Kevin Bacon Number
Kevin Bacon's Kevin Bacon Number is 0
An actor X (other than Kevin) has a Kevin Bacon Number = minimum { Kevin Bacon Number of all actors who appeared some movie with X} + 1
Meryl Streep's number is 1 (The River Wild)
Clint Eastwood's number is 2 (Clint Eastwood in Trouble with the Curve with Jon Gould in R.I.P.D with Kevin Bacon)
Example of a collection of pairwise connections.
Graphs used to model the data.
Graph algorithms used to query the data.
A Graph consists of a set of vertices and edges.
Each edge connects two vertices (but if loops are allowed, then an edge can connect a vertex to itself).
In the Kevin Bacon game, each vertex is either the name of a Movie or of an actor.
In this case
A path in a graph from one vertex to another vertex is a sequence of edges connecting the vertices. The length of a path is the number of edges.
The Kevin Bacon Number of an actor is the length of the shortest path in the Movie-Actor graph from the actor vertex to the Kevin Bacon vertex.
As for the Kevin Bacon Game, data can often be modeled as a graph.
Queries about the data may often be answered by algorithms such as:
There are two basic ways to represent directed graphs. Both ways also work for undirected graphs with no modification required (although some space could be eliminated).
Two Ways of Representing Graphs
1. adjacency matrix. A |V| x |V| sized matrix, A
For unweighted graph,
A[i][j] is 1 if there is an edge from vertex i to vetex j
0 otherwise.
For weighted graph,
A[i][j] is the weight of the edge if there is an edge from
vertex i to vetex j
otherwise some chosen value not to be confused with
a weight (e.g., largest or smallest possible int
value)
(Note for an undirected graph, the matrix A represents the same
edge twice since A[i][j] will be equal to A[j][i].)
2. adjacency list. An |V| sized array of lists.
A[i] = list of vertices j for which there is an edge from i to
j.
(Note for an undirected graph, every edge is represented twice.)
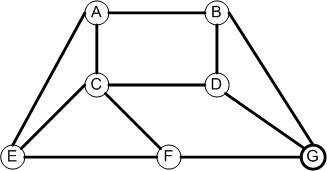
To
A B C D E F G
A 0 1 1 0 1 0 0
B 1 0 0 1 0 0 1
C 1 0 0 1 1 1 0
From D 0 1 1 0 0 0 1
E 1 0 1 0 0 1 0
F 0 0 1 0 1 0 1
G 0 1 0 1 0 1 0
Row k is the same as column k for each k. Why?
From To
A: -> B,C,E
B: -> A,D,G
C: -> A,D,E,F
D: -> B,C,G
E: -> A,C,F
F: -> C,E,G
G: -> B,D,F
Each edge appears on 2 lists. Why?
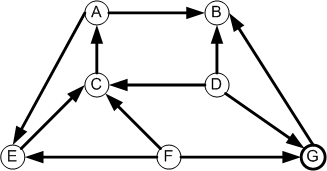
To
A B C D E F G
A 0 1 0 0 1 0 0
B 0 0 0 0 0 0 0
C 1 0 0 0 1 0 0
From D 0 1 1 0 0 0 1
E 0 0 0 0 0 0 0
F 0 0 1 0 1 0 1
G 0 1 0 0 0 0 0
Row 1 is not the same as column 1 for this directed graph. Why?
A: -> B,E
B: -> -
C: -> A,E
D: -> B,C,G
E: -> -
F: -> C,E,G
G: -> B
Each edge is on how many lists?
In many applications where the data is modeled by a graph, the number of edges is typically NOT dense. That is, it is much smaller than in a complete graph where every pair of vertices is connected by an edge.
This means the adjacency matrix would be very sparse (lots of 0's) and some properties would not be very efficient; e.g. getting the degree of a vertex must examine all N entries in a row even though many will be 0.
Adjacency lists are often chosen for the representation. (See section 4.1 for more discussion of why/when this is the better choice.)
public class Graph
{
private final int V; // number of vertices
private int E; // number of edges
private Bag<Integer>[] adj; // adjacency lists
public Graph(int V)
{
this.V = V; this.E = 0;
adj = (Bag<Integer>[]) new Bag[V]; // Create array of lists.
for (int v = 0; v < V; v++) // Initialize all lists
adj[v] = new Bag<Integer>(); // to empty.
}
public Graph(In in)
{
this(in.readInt()); // Read V and construct this graph.
int E = in.readInt(); // Read E.
for (int i = 0; i < E; i++)
{ // Add an edge.
int v = in.readInt(); // Read a vertex,
int w = in.readInt(); // read another vertex,
addEdge(v, w); // and add edge connecting them.
}
}
public int V() { return V; }
public int E() { return E; }
public void addEdge(int v, int w)
{
adj[v].add(w); // Add w to vb <pre></pre>s list.
adj[w].add(v); // Add v to wb <pre></pre>s list.
E++;
}
public Iterable<Integer> adj(int v)
{ return adj[v]; }
}
Find all the vertices connected to a given vertex.
Create a class that supports some collection graph queries of interest. For example: support search for vertices connected to a given vertex.
The class constructor takes a graph (and in this case) the given vertex.
The constructor processes the graph to initialize members that allow supports its allowed queries.
Problem: Find all the vertices connected to a given vertex.
Class:
public class DepthFirstSearch
{
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G, int s)
{
marked = new boolean[G.V()];
dfs(G, s);
}
private void dfs(Graph G, int v)
{
marked[v] = true;
count++;
for (int w : G.adj(v))
if (!marked[w]) dfs(G, w);
}
public boolean marked(int w)
{ return marked[w]; }
public int count()
{ return count; }
}
Is vertex v is connected to s in graph G?
DepthFirstSearch g = new DepthFirstSearch(G, s);
boolean answer = g.marked(w);
The private dfs(G, v) method traverses ALL the vertices that are connected to v by some path.
The count() method returns the number of such vertices; i.e., it returns the number of vertices in the connected component containing v.
0: 1, 2, 5
1: 0, 2
2: 0, 1, 4
3: 4, 5
4: 2, 3
5: 0, 3
Trace the execution of dfs(G, 0)
G
0: 1, 2, 5
1: 0, 2
2: 0, 1, 4
3: 4, 5
4: 2, 3
5: 0, 3
Trace of dfs(G, 0)
vertex marked array
0 1 2 3 4 5
0 x
|
1 x
|
2 x
|
4 x
|
3 x
|
5 x