To Lecture Notes

IT 223 -- 2/21/11

Review Questions

1. How do you compute the expected value of a random variable?

   Ans: Compute the weighted average of the outcomes, weighted by the probability of each outcome:

   E(x) = x₁ p₁ + ... + x_n p_n

2. Intuitively, what does the expected value mean.

   Ans: The long run average of the outcomes of the random variable over a very large number of trys.

3. What is the expected value of a Bernoulli random variable?
   E(x) = x₁ p₁ + x₂ p₂ = 0(1 - p) + 1p = p

4. State the Multiplication Rule for probabilities.

   Ans: If the events A and B are independent, then P(A and B) = P(A) P(B)

5. When flipping a fair coin, what is the probability of
   1. getting at exactly 5 heads in a row?

      Ans: (1/2)⁶ = 1/64. The sequence must be HHHHHT

   2. getting at least 5 heads in a row?

      Ans: (1/2)⁵ = 1/32. The sequence must be HHHHH; we don't care what the next outcome is.

   3. obtaining the sequence THTTH?

      Ans: (1/2)⁵ = 1/32

6. The Paradox of Chévalier de Méré:
   1. Roll a die 4 times. What is the probability of getting at least one ace (1)?

      Ans: 1 - (1 - 1/6)⁴ = 0.5177 = 51.8%

   2. Roll a pair of dice 24 times. What is the probability of obtaining snakeeyes (pair of aces at least once)?

      Ans: 1 - (1 - 1 / 36)²⁴ = 0.4914 = 49.1%

7. An American roulette wheel contains 38 pockets: 18 red pockets, 18 black pockets, and two green pockets labeled 0 and 00. European roulette wheels have only one green pocket labeled 0. Here is an online European roulette game to see what it is like.

   If you bet on red or black, here are the payoff tables for an American roulette wheel:

   Bet on Red Outcome Payoff Probability Red +1 18/38 = 0.474 Black -1 18/38 = 0.474 Green -1 2/38 = 0.052

   Bet on Black Outcome Payoff Probability Red -1 18/38 = 0.474 Black +1 18/38 = 0.474 Green -1 2/38 = 0.052

   What is the expected payoff of playing on red? playing on green.

   Ans: Playing on red is E(x) = 1(0.474) + (-1)(0.474) + (-1)(0.052) = -0.052. You lose about 5 cents each time you play.

8. The following urns contain 6 tickets each. In which urns are letter independent from color. In other words, in which urns are the probabilities of the letters the same whether or not you know the color.

   

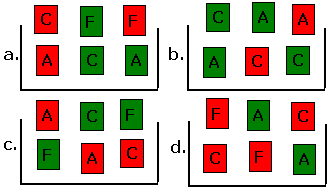
   Ans: In a and b, letter is independent of number. To show that letter and number are independent, you need to show that for each letter value L P(L) if you don't know the color = P(L) for a given color.

   For example, in Problem 8a, if you don't know the color, P(A) = P(B) = P(C) = 2/6 = 1/3. If you know the color is red, P(A) = P(B) = P(C) = 1/3. If you know the color is green, the probabilities are also 1/3.

   In Problem 8c, if you don't know the color, P(F) = 2/6 = 1/3. If you know that the color is green, P(F) = 2/3 = 2/3, so color and letter are not independent.

   To show that two events are not independent, it is enough to find one case where the probabilities are different; to show that two events are independent, you must show that the probabilities are the same for all choices of color and letter.

9. Are these events independent?
   Person A lives at least 20 more years after February 21, 2011.

   Person B lives at least 20 more years after February 21, 2011.

   Ans: It is hard to know. If the people know each other, their lives and life choices can affect each other so A and B are probably not independent. If the people do not know each other, A and B may be independent, but they may also be related in unexpected ways.

10. If the probability of getting struck by lightning in a year is 1/300,000, what is the probability of getting struck by lightning twice in a year?

    Ans: (1 /300,000)² = 1 / 90,000,000,000.

11. If the probability of getting a cold in a given week is 3%, what is the probability of getting at least one cold in a year?

    Ans: 1 - (1 - p)^n = 1 - (1 - 0.03)^52 = 0.7948 = 79%.

12. Estimate the probability that an amateur golfer that plays one round a week makes at least one hole in one on a certain par 3 hole in 50 years. The golfer hits the green 10% on that hole of the time, which has an area of about 4,000 square feet. The hole on a golf green has an area of 14.2 square inches.

    Ans: First estimate the probability of a hole in one in a single try. The area of the hole in square feet is 14.2/144 =0.0986 ft². If the area of the green is 4000 ft², the probability of a hole in one is 0.1 * 0.0986 / 4000 = 2.465 × 10^-6. This the probability of getting at least one hole in one in 50 years is

    1 - (1 - 2.465 × 10^-6)^{(50 * 52)} = 0.006389 = 0.64%

    In practice the probabily will be somewhat higher. The ball can land at a point on the green and then roll into the hole. Suppose that the ball can roll a distance of 50 times the diameter of the hole. This raises the probablity of a hole in one on a single roll by a factor of 50. The revised probability of a hole in one in 50 years is
    1 - (1 - 50 × 2.465 × 10^-6)^{(50 * 52)} = 0.274218 = 27%

The Addition Rule for Mutually Exclusive Events

• Two events A and B are mutually exclusive if A and B cannot both occur at the same time.

• Example 19:   "Obtaining a 1 with one roll of a die" and "obtaining a 2 with one roll of a die" are mutually excusive.

• Example 20:   In a baseball game, "getting a hit in one at bat" and "getting a base on balls" in one at bat are mutually exclusive.

• The Addition Rule:   If A and B are mutually exclusive events, then
  P(A or B) = P(A) + P(B)

• Example 21:   If A is "obtaining a 1" and B is "obtaining a 2", since A and B are mutually exclusive, P(A or B) = P(A) + P(B) = 1/6 + 1/6 = 1/3. However, P(A and B) = 0.

The Standard Deviation of a Random Variable

• We already know the definition of the expected value:
  E(x) = x₁ p₁ ... x_n p_n

• The textbook uses the symbol μ_x instead of E(x).

• The variance of a random variable is denoted by Var(x):
  σ_x² = E[(x - E(x))²] = (x₁ - E(x))² p₁ + ... + (x_n - E(x))² p_n

• The textbook uses the symbol σ_x² instead of Var(x).

• The standard deviation of a random variable is denoted as σ_x. It is the square root of the variance:
  σ_x = √Var(x)

Practice Problems

1. Recall that the expected value for the Rainfall on a Tropical Island example is 1.1 inches. Here is the probability distribution:

   Rainfall	Probability
   0	0.3
   1	0.4
   2	0.2
   3	0.1

   Compute the variance and standard deviation of this random variable.

   Ans: (0 - 1.1)² 0.3 + (1 - 1.1)² 0.4 + (2 - 1.1)² 0.2 + (3 - 1.1)² 0.1
   = 1.21 × 0.3 + 0.01 × 0.4 + 0.81 × 0.2 + 3.61 × 0.1 = 0.89
   The standard deviation is sqrt(0.89) = 0.943

2. Compute the variance and standard deviation of a Bernoulli random variable.

   Ans: The mean of a Bernoulli random variable is 0(1 - p) + 1p = p.

   Variance = (0 - p)² (1-p) + (1 - p)² p = p²(1-p) + (1 - 2p + p²)p
   = p² - p³ + p - 2p² + p³ = p - p² = p(1 - p)

   The standard deviation is he square root of the variance = √p(1 - p)

3. Use your result in Problem 2 to obtain the mean and standard deviation of the number of heads obtained in a single coin flip.

   Ans: E(x) = p = 0.5; σ_x = √0.5(1-0.5) = √0.25 = 0.5

1. E(cx) = c E(x)

2. E(x + y) = E(x) + E(y)

3. E(x₁ + ... + x_n) = E(x₁) + ... + E(x_n)

4. Var(x) = E(x²) - E(x)²

5. Definition:   x and y are independent if E(xy) = E(x)E(y).

6. If x and y are independent, Var(x + y) = Var(x) + Var(y)

• Here are the derivations.