To Lecture Notes

IT 223 -- 1/17/10

Review Questions

1. When is the mean better than the median?

   Ans: When the histogram of the dataset is normal: symmetric and there are no outliers.

2. When is the median better than the mean?

   Ans: When the histogram is skewed and/or there are outliers.

3. Draw the following histogram:

   Bin	Percent
   [0,1)	20
   [1,2)	30
   [2,3)	20
   [3,5)	20
   [5,9)	10

   Since the bin widths are not all equal, the area of a rectangle represents the frequency, not the height. Now answer these questions about the histogram:

   1. Without doing any calculations, what is the median of the histogram in Problem 3?

      Ans: The median is exactly at 2 (50% of observations to the left, 50% to the right).

   2. Is the mean in Part a greater than or less than the median?

      Ans: It is greater then the median. The long tail pulls the mean to the right. The exact value of the mean is computed as this weighted mean:

      _   0.5*20 + 1.5*30 + 2.5*20 + 4.0*20 + 7.0*10   254
      x = ------------------------------------------ = --- = 2.54
                     20 + 30 + 20 + 20 + 10            100
      

   3. What is your best estimate of the percentage of observations in these bins?
      a. [4,5)    b. [7,8)    c. [4,6)

      Ans: 10, 2.5, 12.5.

4. Explain the difference between SD and SD+.

   Ans: The formula for SD uses n in the denominator before taking the square root; the formula for SD+ uses n-1. Most statisticians use SD+ because it takes into account of the extra variability that results in using x to estimate μ.

5. Without doing any calculations, compute the SD for each of these datasets:
   1. 4    4    4    4    4   Ans: 0.

   2. 0   0   0   0   10   10   10   10   Ans: SD is exactly 5; SD+ is a little more than 5, actually 5.35.

6. What happens to the SD of a dataset if
   1. every observation is increased by 7?   Ans: SD is unchanged.

   2. every observation is multiplyed by 3?   Ans: SD is multiplied by 3.

   3. the largest observation is increased by 1000?   Ans: SD increases, but it is hard to say by how much.

7. If SD = 6.94 and n = 23, what is SD+?

   Ans: SD = sqrt(SS / n), where SS = sum of squares of deviations. Solve 6.94 = sqrt(SS / 23) for SS: SS = 1107.76. Then SD+ = sqrt[SS / (n - 1)] = sqrt(1107.76 / (23 - 1)) = 7.06.

8. Compute the mean absolute deviation (MAD) of this dataset:
   20    10    15    15

   Ans: 2.5

9. Do the following for t2 variable of the Micrometer dataset (micrometer.xls). t2 are the measurements of paper thicknesses in mm, made by the professor.
   1. Compute x and SD+.

      Ans: Analyze >> Descriptive Statistics >> Descriptives.

   2. Create a histogram with 5 bins.

      Ans: Graphs >> Chart Builder. Drag a Simple Histogram in to the Chart Preview Area.

   3. Create a scatterplot of t2 vs. the observation number.

      Ans: Graphs >> Chart Builder. Drag a Simple Scatterplot into the Chart Preview Area.

10. How do you sort an SPSS dataset?

    Ans: Data >> Sort Cases. Set the Sort Order to Ascending or Descending as you prefer.

11. The following scatterplots are plots of x_i (measurement) vs. i (observation number) with the sample mean marked with a red horizontal line. The measurement is plotted on the vertical axis; the observation number is plotted on the horizontal axis. What does each plot tell you? Describe each plot using these terms:
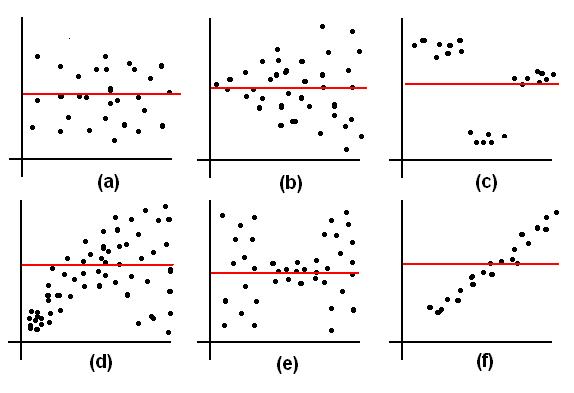
    Unbiased   The average of the observations in every thin vertical strip is the same all the way across the scatterplot.

    Biased   The average of the observations changes, depending on which thin vertical strip you pick.

    Homoscedastic   The variation (SD+) of the observations is the same in every thin vertical strip all the way across the scatterplot.

    Heteroscedastic   The variation (SD+) of the observations in a thin vertical strip changes, depending on which vertical strip you pick.

    

    Ans: (a) unbiased and homoscedastic, (b) unbiased and heteroscedastic, (c) biased and homoscedastic, (d) biased and heteroscedastic, (e) unbiased and heteroscedastic, (f) biased and homoscedastic.

The Ideal Measurement Model

• No measurement is perfect.

• Every measurement involves some random error and systematic bias.

• See this document for more details on the ideal measurement model.

• This document contains information on the official definitions of the meter, second, and kilogram.

Standard Error of the Average

• Because of the random errors involved in the ideal measurement model, the sample mean x will change if the experiment is repeated.

• For the ideal measurement model, x is an estimate of the true measurement μ, we want to know how accurate this average is if the experiment were repeated multiple times.

• There are two ways to estimate how accurately x estimates μ:
  Method 1:   Replicate the experiment several times, compute x for each experiment, then compute the SD+ of the xs. Disadvantage for Method 1: replicating the experiment can be expensive.

  Method 2:   Use the formula for the standard error of the mean or standard error of the average:

  SE_ave = SE_mean = SD+ / √n

  Advantage for Method 2: No replications of the experiment are required. Disadvantage for Method 2: This formula is less accurate than Method 1 if bias is present.

• To find the standard error of the average (SE_ave) using SPSS:
  Analyze >> Descriptive Statistics >> Descriptives

Practice Problems

1. If the data in a dataset with n = 36 follow the ideal measurement model SE = 6.12, what is SE_ave?

2. Use SPSS to compute SE_ave for t2 of the Micrometer Dataset.

The Normal Distribution

• The normal distribution is ubiquitous in statistics.

• Since the sample mean is defined as
  x = x₁ / n + ... + x_n / n,

  it is the sum of independent random variables. Because of the Central Limit Theorem, x is approximately normally distributed if n is large enough.

• Not only is often x approximately normally distributed if an experiment is repeated many times, many other random variables are normally distributed, thanks to the Central Limit Theorem.

• Here is a discussion of The Normal Distribution.