Heap

 

Heaps

When we were working with Binary Search Trees, we were able to take advantage of their special properties - that everything to the left of a node is less than that node, and everything to the right of a node is greater than that node - to provide more efficient handling of ordered data. Now we are going to introduce another kind of binary tree which has special properties that allow us to perform certain operations more easily.

A heap is a tree structure where the relationship is between the parent and its children. In a min-heap, the parent always has a smaller value than its children (there is no ordering among the children themselves), so the minimum value in the tree will be at the root. In a max-heap, the parent always has a greater value than its children, so the maximum value in the tree will always be at the root. This property allows us to efficiently implement a priority queue, which is a queue where the item with the highest priority is dequeued first. (A normal FIFO queue is like a priority queue where items that were entered first have higher priority.)

In addition to the relationship between the parent and its children, we will impose another property on heaps. Heaps will always have to be full trees -- that is, there must be no holes at any depth except for the greatest depth, and all of the holes at the greatest depth are to the right. (That is, we will fill the tree from top to bottom, and from left to right.) This restriction on the shape of the tree will make our implementation easier and more efficient, as we will see later.

Inserting Into A Heap

As with a Binary Search Tree, when we insert into a heap we need to make sure that the resulting structure is still a heap. So the resulting structure needs to maintain the relationship between each node and its children, and the resulting tree cannot have any holes in it anywhere except for the bottom right of the tree. We will always initially use the first available spot (the leftmost open spot at the bottom of the tree) to initially insert the new item into the heap, so the tree will continue to be full after we insert. But will it still be a heap?

Let's look at an example of constructing a min-heap:

We will begin by inserting 70 into the heap. Since this is the first item in the heap, it will have to be the root.

Next, we will insert 150 into the heap. Since the tree is full at depth 1 (the root), we will insert it in the leftmost spot at depth 2, which in this case is the root's left child. Since 70 < 150, this is still a heap.

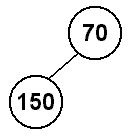
Now we will insert 110 into the heap. The next available spot to add an item to the heap is roots right child, so we will add 110 there. This is also still a heap because 70 < 110. (Remember, it does not matter how the siblings relate to each other.)

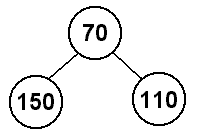
Next, we will insert 80 into the heap. Since the tree is now full at depth 2, we will add 80 at the leftmost spot at depth 3 (150's left child). This presents a problem, though, because 150 > 80, so we no longer have a heap.

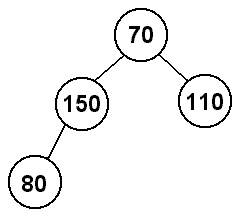
How do we make this a heap again? Whenever we insert, we have to look at the new node's parent and check the relationship. If the new node is smaller than its parent (in a min-heap), then we will swap the two values. After we have done this, we then have to check if the new one is smaller than its new parent. We continue this process of checking and swapping until we either hit the root or reach a spot where the new value is greater than its parent, because in either case we will have a heap again.

So, when we insert 80, we will have to swap it with the 150 since 150 > 80. 80's parent will now be 70, so we will stop there since 70 < 80.

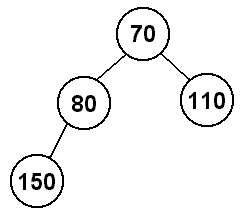
Now let's add 30 to the heap. This will start in the second spot at depth 3 (80's right child), and then will have to swap with 80 because 80 > 30, and then will also swap with 70 because 70 > 30, so here 30 will become the new root of the heap. This is consistent with our idea of a min-heap, since 30 is now the smallest value in the heap.

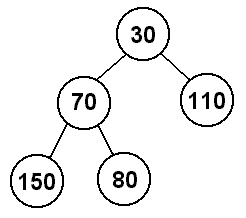
Finally, we will add 10 to the heap. It will start in the third spot at depth 3 (110's left child), and we will have to swap it with 110 because 110 > 10, and then we will also have to swap it with 30 because 30 > 10, so now 10 becomes the root of the heap.

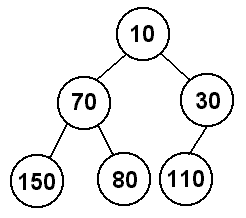
So, when we insert something into the tree, we initially place the item in the bottom, leftmost spot in the tree, and then swap the new value with its parent until we once again satisfy the properties of the heap.

Removing From A Heap

When we remove an item from the heap, we will always take the value at the root. Why? The reason we use a heap is to have easy access to the item that has the highest or lowest value in the current set of items. Like the stack and the queue, limiting the possible behavior of the heap ensures that it will behave consistently.

When we remove the item at the top of the heap, we leave an empty spot. Since the heap cannot have any holes in it except at the bottom-right, we no longer have a heap, so what can we do to reestablish a heap?

Our first concern is that the root of the heap gets the lowest value in the tree. Luckily, we can narrow our search for that value to the root's children. Why can we do this? Well, we know that in a min-heap the parent has a smaller value than its children, so all of the values below root's left child must have a greater value than root's left child, and all of the values below root's right child must have a greater value than root's right child. This means that the minimum value in the heap will be either root's left child or root's right child. That means we can promote the minimum of root's children to the root of the heap.

In this case, that means that 30, the right child of the root, will be moved to the top of the heap.

Now there is a hole where the 30 was, so we will again have to move one of its children up the heap. Since there is only a left child, 110, we will move that to where 30 was.

We are left with a tree that satisfies the properties of the heap, so we are done. Unfortunately, it is not always this easy. Suppose we have the following heap:

If we remove the minimum value, the 70, we will replace it with the 80, and then replace the 80 with the 130. That would leave us with:

The tree we are left with is not a heap, because there is a hole on the bottom left of the tree. So what should we do in this situation? Well, if we are going to have holes in the tree, they should be at the bottom of the tree and to the right of all the values. To fill in this hole, then, we will take the last value in the heap (the bottom rightmost value) and move it to where the hole is.

We've gotten rid of the hole, but now the relationship between parents and children is not maintained because 130 > 110. So, after we fill in the hole, we have to once again move up the tree swapping with the parent until the parent is smaller.

Now, we finally have a heap. To review, first we remove the value from the root of the heap, and then work our way down the tree replacing the removed value with the smaller of the two children. Next we move the last value in the heap to fill in the hole (if there is a hole). Finally, we swap up the tree like we did in the insert so that the tree we are left with still satisfies the properties of a heap.

Implementing A Heap With A Vector

Up until now, we have been talking about heaps as trees, but how would we implement them? Using a tree to implement the heap leaves us with some questions that have difficult answers. How do the children know who their parent is? How do you keep track of where the next item should be added? In order for children to interact with their parent, we would have to use recursion to go down a path, and then as the recursive calls unfold swap back up the tree to restructure the heap. To keep track of where the next item should go, we could keep a count of the number of items in the heap, and use that number to construct the path down the tree to insert.

Both questions have reasonable answers, but in practice they require complicated code in order to work correctly.

So if we are not going to store the heap as a tree, how should we store it? Before we decide how to store it, let's number the spots in the heap as follows:

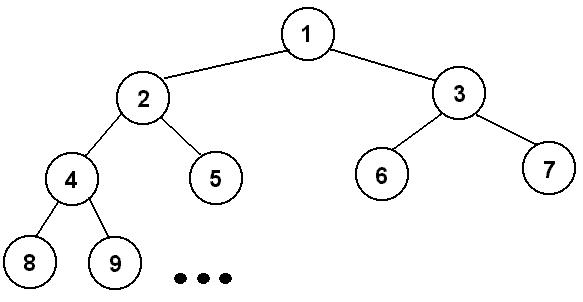
We have numbered the items in the heap from top to bottom and from left to right with no gaps in the numbering. These should resemble indexes for the spots in the Heap. The indexes themselves are not what makes this numbering system so valuable. If you look closely, you will notice the following two relationships: the left child's index is exactly twice the parent's index, and the right child's index is twice the parent's index + 1. This means that we can easily get from the parent to one of its children, and we can also easily get from the children to the parent by simply dividing by two. This relationship between the indexes is what makes it possible for us to implement our heap using a Vector.

When we numbered the items in the heap, we started with the root at 1 rather than 0. This simplifies our math considerably, but if we are using a Vector indexes start at 0. What should go in index 0 if the root is at index 1? The easiest solution is to just throw a "null" into index 0 and effectively throw that part of the Vector away. We could start the root at 0, but that complicates the math, and throwing away one index in a Vector is not really a significant waste of memory.

Heapsort

Now that you know what a Heap is, let's talk about a sorting algorithm called Heapsort.

The Heapsort algorithm starts with an array, or vector, full of random numbers. Here's the algorithm for Heapsort:

1. Make the vector into a heap.
2. Sort the heap.

If you want your vector sorted from least to greatest, first make it into a max heap.
If you want your vector sorted from greatest to least, first make it into a min heap.

How Heapsort Works

We start out with an empty heap, and treat the data in the vector as if we are adding them one at a time. For our example, we'll first make the vector into a min heap, and then use the min heap to sort the vector from greatest to least. You can easily do the opposite (max heap, least to greatest).

0 1 2 3 4 5 6 7 8
X 9 2 1 3 6 5 4 7

We add the 9 to the empty heap. The heap was empty, so this becomes the top of the heap.

0 1 2 3 4 5 6 7 8
X 9 2 1 3 6 5 4 7

Next we add the 2 at index 2.

0 1 2 3 4 5 6 7 8
X 9 2 1 3 6 5 4 7

After we add 2, we need to swap up the tree. In this case, 2 is smaller than its parent 9, so we need to swap them.

0 1 2 3 4 5 6 7 8
X 2 9 1 3 6 5 4 7

2 is now at the root, so the first two elements are now a heap. We insert 1 at index 3.

0 1 2 3 4 5 6 7 8
X 2 9 1 3 6 5 4 7

1 is at index 3, so its parent is at index 1. Index 1 contains 2, so we need to swap.

0 1 2 3 4 5 6 7 8
X 1 9 2 3 6 5 4 7

Now we add the 3 at index 4.

0 1 2 3 4 5 6 7 8
X 1 9 2 3 6 5 4 7

3 is at index 4, so its parent is at index 2, which is the 9, so we need to swap.

0 1 2 3 4 5 6 7 8
X 1 3 2 9 6 5 4 7

3 is now at index 2, whose parent is 1, and the value at index 1 is 1, so we do not need to do any more swaps. Now we can add the 6 at index 5.

0 1 2 3 4 5 6 7 8
X 1 3 2 9 6 5 4 7

6 is at index 5, so its parent is index 2, which contains 3, so we do not need to swap. Next we add the 5 at index 6.

0 1 2 3 4 5 6 7 8
X 1 3 2 9 6 5 4 7

5 is at index 6, so its parent is index 3, which contains 2, so we do not need to swap. Now we add the 4 at index 7.

0 1 2 3 4 5 6 7 8
X 1 3 2 9 6 5 4 7

4 is at index 7, so its parent is also index 3, so we do not need to swap because 4 > 2. Finally, we add 7 at index 8.

0 1 2 3 4 5 6 7 8
X 1 3 2 9 6 5 4 7

7 is at index 8, so its parent is at index 4, which is the 9, so we need to swap them.

0 1 2 3 4 5 6 7 8
X 1 3 2 7 6 5 4 9

7 is now at index 4, so its parent is index 2, which contains 3, so we do not need to swap anymore. This is the end of the input, so what is left is a heap containing all of the original data.

Now that we have a heap, we can begin sorting the values. We do this by removing the minimum value of the heap and moving it to the spot that was the last spot in the Vector. When we call removeMin(), the heap becomes one smaller, so the last spot becomes open and we can put the value we removed there.

First, we remove the 1 and move it to index 8.

0 1 2 3 4 5 6 7 8
X 2 3 4 7 6 5 9 1

Next, we remove the 2 and move it to index 7.

0 1 2 3 4 5 6 7 8
X 3 6 4 7 9 5 2 1

Next, we remove the 3 and move it to index 6.

0 1 2 3 4 5 6 7 8
X 4 6 5 7 9 3 2 1

Next, we remove the 4 and move it to index 5.

0 1 2 3 4 5 6 7 8
X 5 6 9 7 4 3 2 1

Next, we remove the 5 and move it to index 4.

0 1 2 3 4 5 6 7 8
X 6 7 9 5 4 3 2 1

Next, we remove the 6 and move it to index 3.

0 1 2 3 4 5 6 7 8
X 7 9 6 5 4 3 2 1

Finally, we remove the 7 and move it to index 2.

0 1 2 3 4 5 6 7 8
X 9 7 6 5 4 3 2 1

Since there is only one value left, the 9, it must be in the right position. What we are left with is a sorted list of numbers (in this case sorted from highest to lowest. To get the list from lowest to highest, we would have needed to create a max heap rather than a min heap).