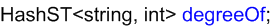There are two basic ways to represent directed graphs. Both ways also
work for undirected graphs with no modification required (although
some space could be eliminated).
Two Ways of Representing Graphs
1. adjacency matrix. A |V| x |V| sized matrix, A
For unweighted graph,
A[i][j] is 1 if there is an edge from vertex i to vetex j
0 otherwise.
For weighted graph,
A[i][j] is the weight of the edge if there is an edge from
vertex i to vetex j
otherwise some chosen value not to be confused with
a weight (e.g., largest or smallest possible int
value)
(Note for an undirected graph, the matrix A represents the same
edge twice since A[i][j] will be equal to A[j][i].)
2. adjacency list. An |V| sized array of lists.
A[i] = list of vertices j for which there is an edge from i to
j.
(Note for an undirected graph, every edge is represented twice.)
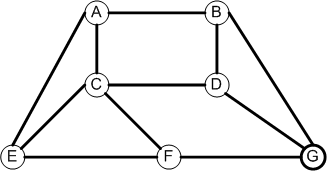
To
A B C D E F G
A 0 1 1 0 1 0 0
B 1 0 0 1 0 0 1
C 1 0 0 1 1 1 0
From D 0 1 1 0 0 0 1
E 1 0 1 0 0 1 0
F 0 0 1 0 1 0 1
G 0 1 0 1 0 1 0
Row k is the same as column k for each k. Why?

From To
A: -> B,C,E
B: -> A,D,G
C: -> A,D,E,F
D: -> B,C,G
E: -> A,C,F
F: -> C,E,G
G: -> B,D,F
Each edge appears on 2 lists. Why?
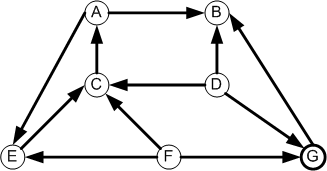
To
A B C D E F G
A 0 1 0 0 1 0 0
B 0 0 0 0 0 0 0
C 1 0 0 0 1 0 0
From D 0 1 1 0 0 0 1
E 0 0 0 0 0 0 0
F 0 0 1 0 1 0 1
G 0 1 0 0 0 0 0
Row 1 is not the same as column 1 for this directed
graph. Why?

A: -> B,E
B: -> -
C: -> A,E
D: -> B,C,G
E: -> -
F: -> C,E,G
G: -> B
Each edge is on how many lists?
This algorithm is applicable to a directed graph whose edges represent
dependencies. It outputs the vertices in an order that respects the
dependencies.
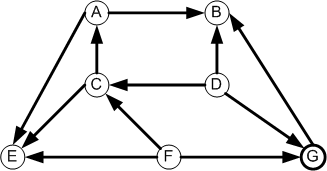
What node or nodes have no prerequisites?
These are the values that can be output first
in topological sort order.
The idea is to first output vertices with no dependencies; that is,
with in-degree = 0.
Once a vertex has been output, we can remove it from the graph and
decrease the in-degree of all its adjacent vertices.
Repeat the process until no more vertices remain with in-degree 0.
If all vertices have been output, then the output order is one of
perhaps several possible topological sorted orders.
If all vertices have not been output, then a cycle exists and
topological sort is not possible.
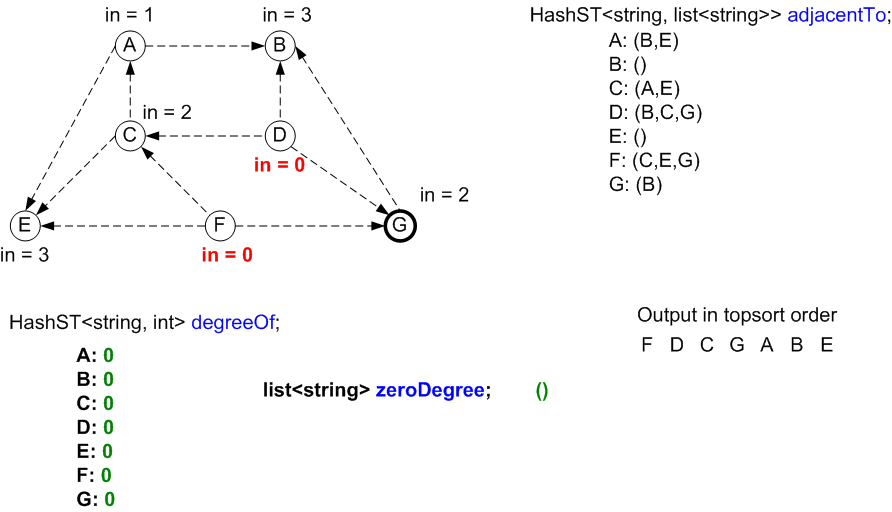
The in-degrees of each vertex are crucial to the algorithm.
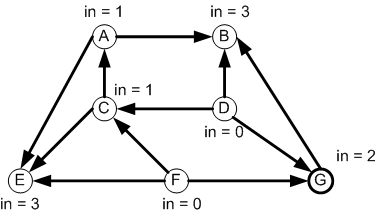
First we have to represent the graph. Note that the in-degrees
are not stored in the representation.
Next, the in-degrees will be computed in a separate data structure:
degreeOf.
An additional separate data structure will be used to hold
vertices that are ready to be output: zeroDegree
The graph can be represented by a HashMap whose
keys are the graph vertices and whose values are
LinkedLists of the adjacent vertices.
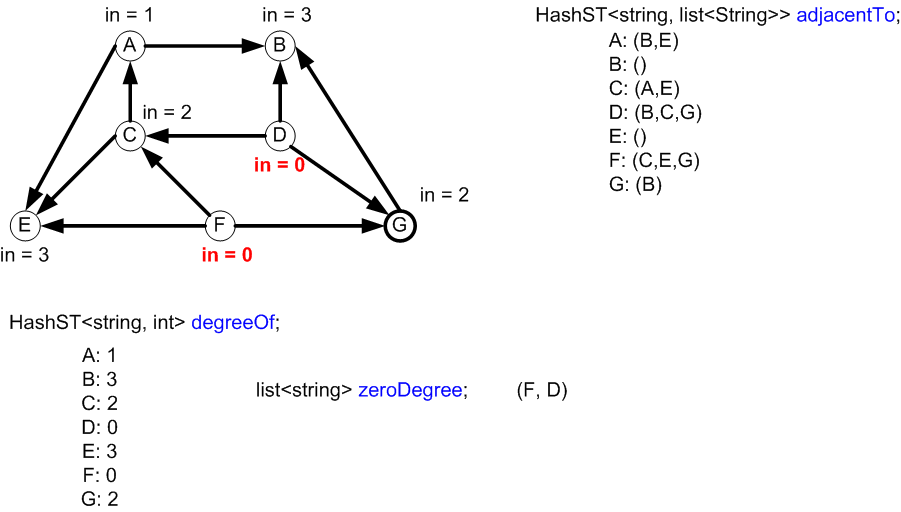
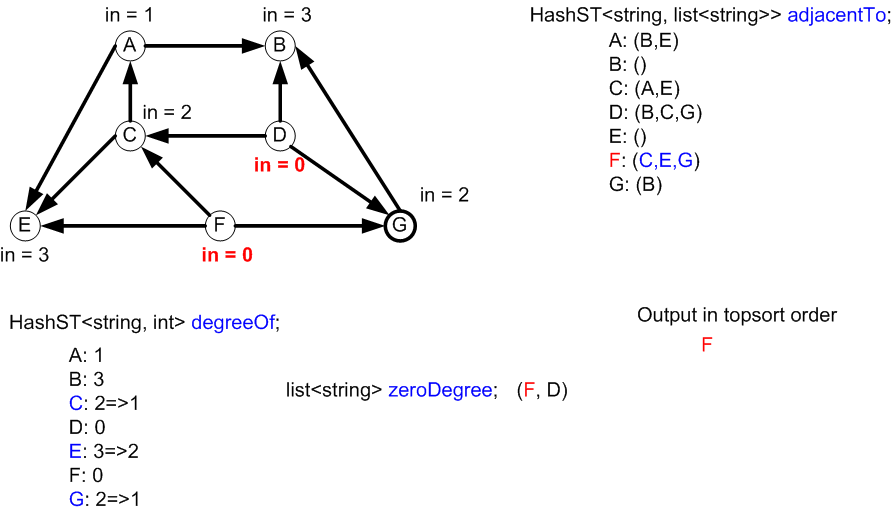
Nothing added to zeroDegree
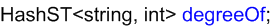
Vertices C and G were added to zeroDegree since their degrees in the
HashMap degreeOf just became 0.
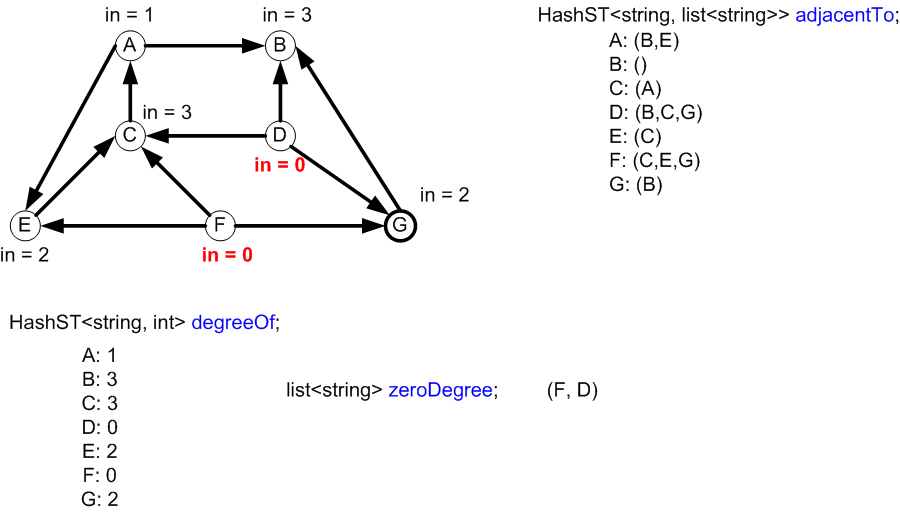
The next node to be output will be C.
Final state:
- The LinkedList zeroDegree is empty.
- All vertices have been output in topological sort order.
- All vertices have 0 degree in the HashMap degreeOf.
- The graph data structures have not changed.
This graph with the direction of one edge reversed now has a
directed cycle.
The initial state of the data structures for topological sort
are shown along with the graph representation.
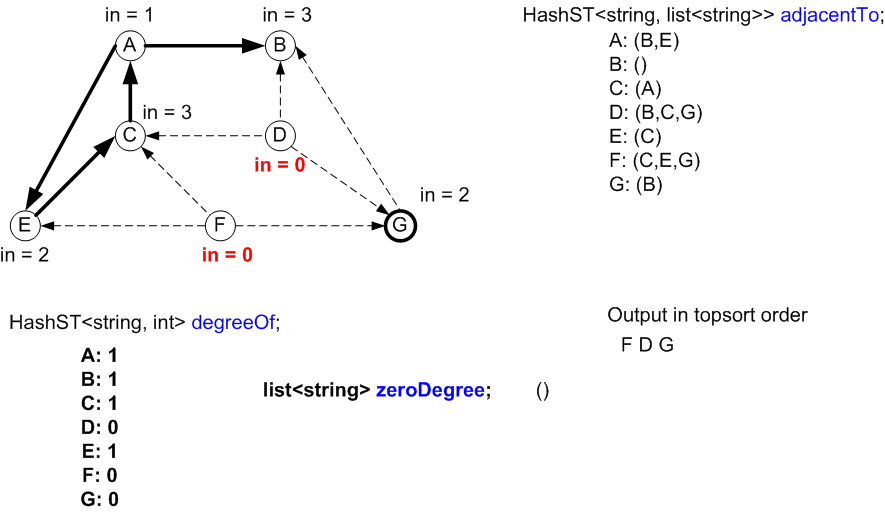
- The algorithm ends when all previous elements in zeroDegree have been
processed and the list is empty.
- However, 4 vertices have not been output.
- The degrees of these 4 vertices in the degreeOf HashMap are not
0.
- This means a cycle exists among those 4 nodes.
Problem: Find the shortest path from V0 to each of the
other vertices in this example weighted undirected graph:
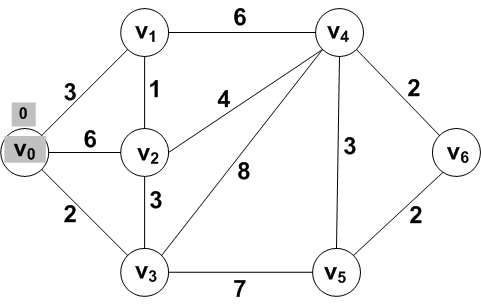
The shortest distance from V0 to itself is
clearly 0.
The shortest distance from V0 to the other
vertices will be determined incrementally.
At each step we will discover one more vertex whose shortest
distance from V0 is known as well as the
path from V0.
The vertices are in three groups:
- Vertices whose shortest distance from V0
is known
-
vertices that are adjacent to some known vertex (the
frontier vertices)
-
all the other vertices (not known, not in the frontier)
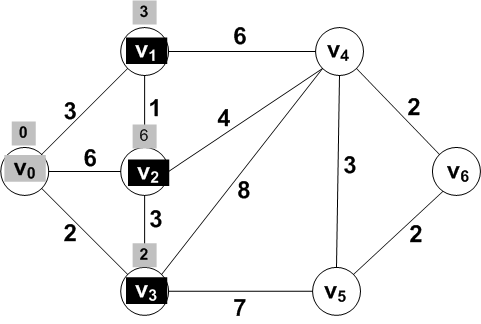
Known: {V0}; Frontier: {
V1, V2,
V3}; Other: { V4,
V5, V6 }
At each step, one frontier vertex can be added to the
known vertices.
Which
frontier vertex can become known in this example?
Answer: Vertex V3 with a distance of
2.
The new known set: {V0, V3}
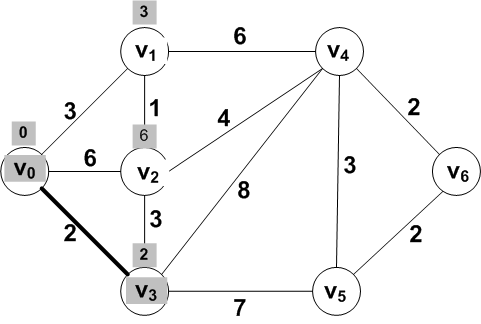
Why is there no shorter distance path, perhaps going
through other vertices?
Known: {V0, V3}; Frontier: {
V1, V2, V4,
V5}; Other: { V6 }
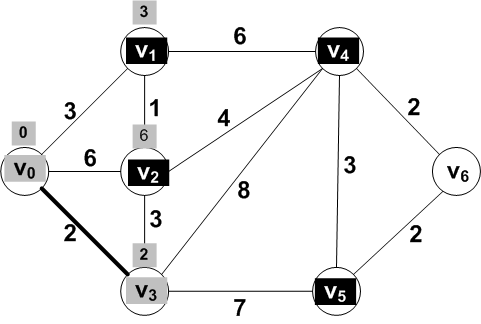
The distances for the known vertices are correct.
But the distances for the frontier vertices should be
updated.
Why? Because, there may now be a shorter path that
goes through the new known vertex
V3.
The new known vertex V3 is adjacent
to frontier vertices V2,
V4, and V5.
Only the distances to these
adjacent vertices V2,
V4 and V5 may require updating.
Vertex V1 was already in the frontier and
had a preliminary distance of 3. But it is not
adjacent to the new known vertex
V3. So adding V3 doesn't
(yet)
give any new path to V1 and its distance
stays the same.
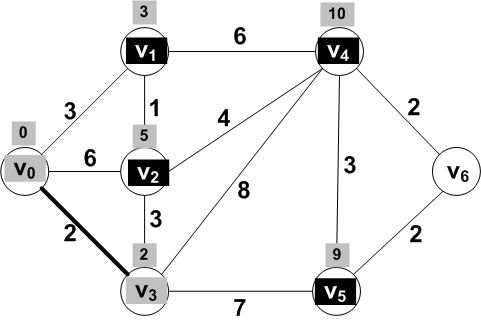
For the vertices adjacent to V3
dist(V0, V2) = ?
dist(V0, V4) = ?
dist(V0, V5) = ?

For the vertices adjacent to V3
dist(V0, V2) = dist(V0, V3) + dist(V3, V2) = 2 + 3 = 5
dist(V0, V4) = dist(V0, V3) + dist(V3, V4) = 2 + 8 = 10
dist(V0, V5) = dist(V0, V3) + dist(V3, V5) = 2 + 7 = 9
After updating the distances the frontier the vertex with the
smallest distance is V1

So V1 should be moved to the known
set of vertices
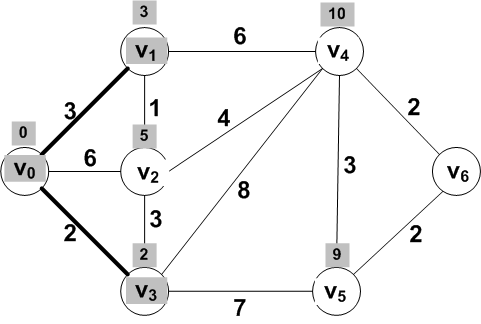
New know vertex: V1
Known vertices: {V0, V1,
V3}
What is the frontier set now?
Which of these frontier vertices should have distances
updated?
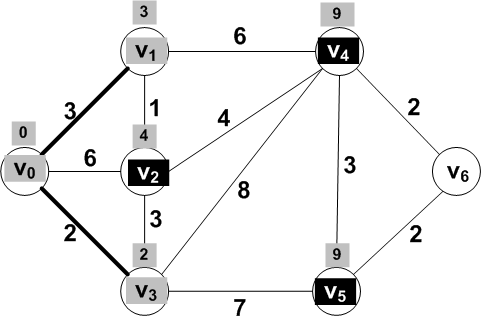
New know vertex: V1
Known vertices: {V0, V1,
V3}
Frontier set: {V2,
V4, V5}
For the vertices V2 and
V4 adjacent to V1, updated
distances are:
dist(V0, V2) = dist(V0, V1) + dist(V1, V2) = 3 + 1 = 4
dist(V0, V4) = dist(V0, V1) + dist(V1, V4) = 3 + 6 = 9

Which frontier vertex should be moved to
known?
Answer: V2
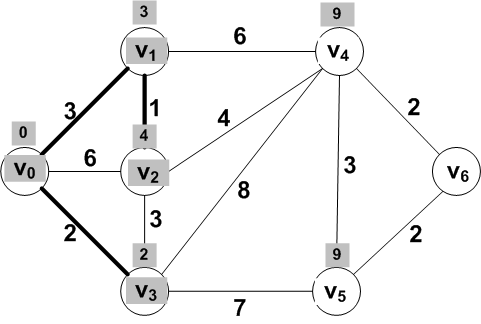
New frontier set:
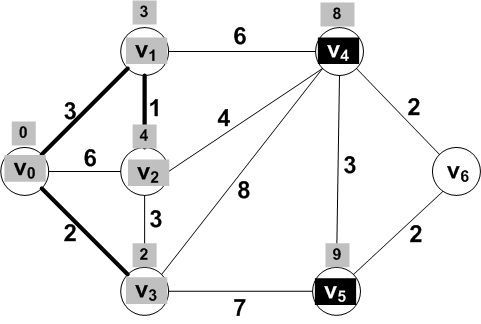
Only V4 adjacent to the new known
vertex V2 was updated.
Frontier vertex V4 has smallest
distance and should be moved to known.
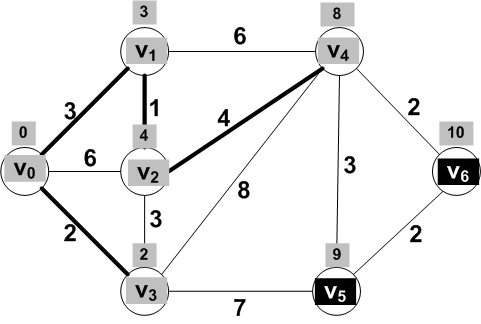
For the frontier vertices V5 and
V6 adjacent to V4, updated
distances are:
dist(V0, V5) = dist(V0, V4) + dist(V4, V5) = 8 + 3 = 11
dist(V0, V6) = dist(V0, V4) + dist(V4, V6) = 8 + 2 = 10
But wait! dist(V0,
V5) was already 9!
So we should not change this distance since the update
through the new known vertex does not give a smaller value.
Final shortest distances from V0 to each of
the other vertices:
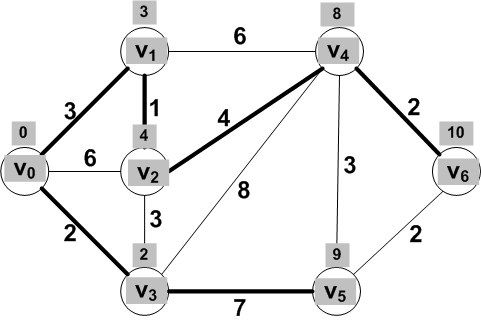
For a new known vertex, update the distance for its adjacent
vertices.
Find the vertex with the minimum distance in the set
of frontier vertices.
Delete the vertex with the minimum distance from the set
of frontier vertices.
What data structure might be used?
The shortest distance solution is an example of a
greedy algorithm.
That is, at each step of the solution, we picked the
smallest
Another problem that can be solved with a greedy
algorithm: minimum cost spanning tree.
Given a weighted graph, find a subset of the edges that forms
a tree and find one that has the minimum total weight
(or cost).
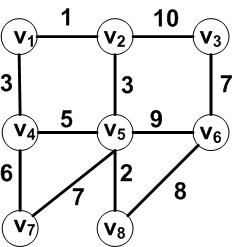
When is a graph a tree?
- Number of vertices = N
- Number of edges = N-1
- No cycles
Visit each vertex exactly once and return to the starting vertex.
Minimize total cost
Greedy algorithm doesn't work!
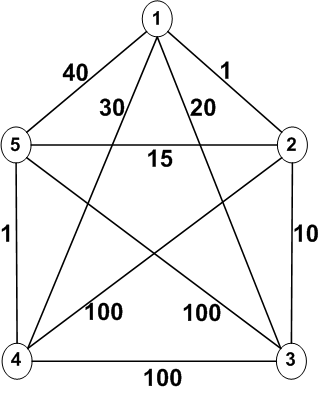
Starting at vertex 1, a greedy algorithm for the traveling
salesman problem below would begin:
1 => 2 => 3
Then the next vertex can't be 1. So the next vertex would have
to be either 4 or 5.
1 => 2 => 3 => 4 => 5 => 1
cost: 1 + 10 + 100 + 1 + 40 = 152
or
1 => 2 => 3 => 5 => 4 => 1
cost: 1 + 10 + 100 + 1 + 30 = 142
But a better path would be to start with the second smallest
cost (20) from vertex 1:
1 => 3 => 2 => 5 => 4 => 1
cost: 20 + 10 + 15 + 1 + 30 = 76