Application: The program reads initially reads Dow
Jones Industrial Average closing averages from a file containing
dates and closing averages. The program then prompts for an input date.
If the stock exchange was open on that date, the closing
average is printed
-
If date is later than the last date read in from the file,
a message is printed and the last recorded date and closing
average are printed.
-
Otherwise, a message is printed that the stock exchange was
closed for the input date, then prints the next recorded date
and its closing average.
Data Structure to store the file data?
Solution using this data structure
Algorithms for ceiling and floor Methods[2] [top]
As for many of the binary search tree methods, these two
methods can easily be implemented either iteratively
(i.e. with loops) or recursively (one public and
one private, recursive method).
Either type of implementation is facilitated by a closer
examination of examples.
Suppose we wish to find
floor(45) // largest key in the tree less than or equal to 45 (or null)
Example 1
60
/ \
50 70
floor(45) = ?
Candidates? Which keys (if any) are smaller than 45? Which one of these
candidates (if any) is largest?
Example 2
40
/ \
/ \
20 60
/ \ / \
10 30 50 70
floor(45) = ?
Candidates? Which keys (if any) are smaller than 45? Which one
of these candidates is largest?
Invariants for the Key floor(Key k) Algorithm[3] [top]
For a binary search tree define invariants t and candiate
t: Node reference to subtree that contains floor or null if no there
is no such subtree.
candidate: Node not in t whose key is the largest key less than the key in t
or null if there is no such Node in the tree.
How should we intialize t and candidate
so that the both descriptions are correct initially?
Assuming both t and candidate are initialized correctly,
as t and candidate are updated, we make sure the invariant
relation is maintained.
In that case how do we compute floor(k)?
Computing Key floor(Key k)[4] [top]
Invariants
t: Node reference to subtree that contains floor of k or else contains no keys
smaller than k.
candidate: Node not in t whose key is the largest key less than k in
the whole tree or null if there is no such Node in the tree.
(Base case) If t is null, floor is candidate
-
If k is equal to t.key, floor is just k.
-
If k is smaller than t.key, then candidate doesn't change,
but t should be updated to be the left subtree, t.left.
-
If k is larger than t.key, then candidate should be updated
to be t.key and t should be updated to be the right subtree, t.right.
Since the subtree referenced by t gets smaller with each
step, this will eventually find the floor.
Java Code outline for Key floor(Key k)[5] [top]
public class BST<Key extends Comparable<Key>, Value>
{
public Key floor(Key k)
{
return floor(k, null, root);
}
/**
* returns the floor of k
* @param k the search key
* @param candidate largest key in the tree but not in subtree t
* that is less than k (might be null)
* @param t subtree that contains the floor of k or that is empty if
* the floor of k is candidate
*
* @return the floor of k in the subtree t or candidate if
* k is larger than all keys in subtree t.
*/
private Key floor(Key k, Key candidate, Node t)
{
/*
* (Base case) If t is null, floor is candidate
* if k is equal to t.key, floor is just k.
* if k is smaller than t.key, then candidate doesn't change,
* but t should be updated to be the left subtree, t.left.
* if k is larger than t.key, then candidate should be updated
* to be t.key and t should be updated to be the right subtree, t.right.
*/
}
}
public class BST<Key extends Comparable<Key>, Value>
{
public Key floor(Key k)
{
return floor(k, null, root);
}
/**
* returns the floor of k
* @param k the search key
* @param candidate largest key in the tree but not in subtree t
* that is less than k (might be null)
* @param t subtree that contains the floor of k or that is empty if
* the floor of k is candidate
*
* @return the floor of k in the subtree t or candidate if
* k is larger than all keys in subtree t.
*/
private Key floor(Key k, Key candidate, Node t)
{
if (t == null) return candidate;
int cmp = k.compareTo(t.key);
if (cmp < 0) {
return floor(k, candidate, t.left);
} else if (cmp > 0) {
return floor(k, t.key, t.right);
} else {
return t.key;
}
}
}
We could add a public printKeys method to BST:
public class BST<Key extends Comparable<Key>, Value>
{
/**
* prints the keys to standard output in sorted order
*/
public void printKeys()
{
printKeys(root);
}
/**
* prints the keys in the subtree t to standard output
* in sorted order
*/
private void printKeys(Node t)
{
/**
* if t is empty, return
* print keys in the left subtree in sorted order
* print t.key
* print keys in the right subtree in sorted order
*/
}
}
Implementing the Iterable<Key> keys() Method[8] [top]
The keys method has to return a reference to some object that
has a method:
Iterator<Key> iterator()
The Iterator<Key> that this iterator() method
returns should allow the keys to be returned, one at a time and in
sorted order, using the next() method.
The Queue<E> class implements
Iterable<E> [Queue has an Iterator<E> iterator() method].
So one implementation of keys() would be to
- Create an empty Queue<Key>
- Insert the keys from BST into this Queue in order.
- return the Queue
public class BST<Keys extends Comparable<Key>, Value>
{
Iterable<Key> keys()
{
Queue<Key> keylst = new Queue<Key>();
addKeys(root, lst);
return lst;
}
/**
* adds the keys in subtree t in order to the end of lst
* @param t the subtree
* @param lst list of keys smaller than the keys in t.
*/
private void addKeys(Node t, Queue<Key> lst)
{
/**
* (Like printKeys, but add to lst instead of printing:
*
* if t is empty do nothing (just return)
* add keys from the left subtree
* add t.key
* add keys from the right subtree
*/
}
}
Final Java Version of Iterable<Key> keys()[10] [top]
public class BST<Keys extends Comparable<Key>, Value>
{
Iterable<Key> keys()
{
Queue<Key> keylst = new Queue<Key>();
addKeys(root, keylst);
return keylst;
}
/**
* adds the keys in subtree t in order to the end of lst
* @param t the subtree
* @param lst list of keys smaller than the keys in t.
*/
private void addKeys(Node t, Queue<Key> lst)
{
if (t == null) return lst;
addKeys(t.left, lst);
lst.add(t.key);
addKeys(t.right, lst);
}
}
Implementing Binary Search Tree Methods Recursively (Hw3)[11] [top]
You are to complete and test the methods in the BSTSet
class.
A JUnit test class, BSTSetTest is provided.
Hints, etc.
You must use recursion. The public method should call a
private method that will need at least 1 more parameter than the
public method - namely, a Node parameter. The public method will
pass root to this parameter.
The private methods that change the tree (remove methods)
should return a Node reference that points to the modified tree
(or subtree) that was passed to it.
-
The private methods that do NOT change the tree (size
methods) typically just return an int.
-
Some public methods return boolean type (isXXX methods). The
corresponding private methods may need to return an integer
to use to test the condition (depending on what the XXX
condition is) as well as whether the condition is true or
not.
For example, the public method:
public boolean isBalancedS()
should return true if at every Node, the size of its left
subtree is the same as the size of its right subtree.
The private isBalancedS method could in principle return
boolean. But at each subtree you need to know 2 things: (1)
are the left and right subtrees themselves size balanced and
(2) do the left and right subtrees have the same size.
If the private isBalancedS method returned boolean, we
would only have the answer for (1). To check (2), we
could call the private size method to get the sizes of
the left and right subtrees. But this means another recursive
descent down into those subtrees!
Solution:
The private isBalancedS should return an int. This value
should be the size of the subtree provided the subtree itself
is size balanced. But if the subtree is not size balanced, it
should return a different value. E.g. -1 will do since the size of a
subtree is always >= 0.
The public isBalancedS() method then just checks whether
the private method returns -1 or not.
This is much more efficient than calling size(t.left) and
size(t.right) at every Node t to check the balance condition
in addition to calling isBalancedS(t.left) and
isBalanced(t.right) to check that the subtrees are themselves balanced.
Some of the size methods ask you to count the number of nodes
satisfying some property. Some of the remove methods ask you to
remove the subtree at nodes satisfying some property. These
properties include:
- whether the node contains an odd integer key
- size of the left and right subtrees
- height of the node
- depth of the node
In the case of the height and depth, the public method has an
int parameter. E.g.
public int sizeAtDepth(int k)
This should return the number of nodes whose depth is k.
What parameters should the recursive private sizeAtDepth method
have? It always needs 1 more, e.g. Node.
The depth of the root is 0 and the depth of a child is 1 more
than its parent. So the depth of nodes can be determined as you go
down the tree.
Recalling the principles
It is easy to pass an additional parameter to the private
method that gives the depth of the subtree at the Node
parameter:
/**
*
* @param t the subtree
* @param k the required depth
* @param d the depth of node t
* @return the number of nodes in the subtree at t that
* have depth k
private int sizeAtDepth(Node t, int k, int d)
What does the public method pass to the private method for
these three parameters?
The sizeAtHeight method seems similar to the sizeAtDepth
method, but the problem is we can't calculate the height of each
node as we go down the tree, only on the way back up. Why?
We could call the recursive private height(Node t) method at every Node,
but this would be very inefficient and add to the recursive calls
of the private sizeAtHeight.
For the size and remove methods whose condition involves the
height, an efficient implementation can be achieved by using an
extra member of the Node to store its height. This avoids the
recursive calls to height(Node t).
Why balanced?
What is the balance condition?
How does balancing affect execution time?
How complicated is the implementation for balancing?
Easy! We want the put and get methods to be O(log(N))
instead of O(N).
The height of a binary search tree is the longest path from the
root to a null link.
The height of a binary search tree with N keys determines the
number of comparisons in the worst case
for both put and get.
If the tree is unbalanced some paths will be short at the
expense of making other paths longer with the worst unbalanced
case where there is only 1 path of length N - 1.
What is the balance condition?[16] [top]
There are a number of possible choices for the balance
condition for a balanced binary search tree:
-
For each node, the number of nodes in its left subtree should
be (almost) the same as the number in its right
subtree. (Not really used. Probably messy to implement.)
(AVL tree) For each node, the heights of its children should differ by
at most 1.
-
(Red Black tree)
Add a "color" property to each node: either black or red.
Then the balance condition requires that all paths from the
root to a null link have the same number of black nodes. Paths
can contain extra red nodes, but with a restriction so that
the length of every path is no greater than 2 times the number
of black nodes in the path.
For the AVL tree or the Red Black tree, the implementation of
the get methods is exactly the same as for an ordinary
(unbalanced) binary search tree.
The put and delete methods that modify the tree
need some additional code to handle the balancing.
For example, for the put method, going down the tree
(searching) and creating a new Node when the null link is found is
also exactly like the ordinary unbalanced binary search tree
code.
Returning back up the tree and attaching the modified subtree
is where code needs to be inserted to check if the addition to the
subtree requires rebalancing.
This rebalancing code may take place at each node on the way
back up the tree and so the effect on execution time depends on
this code being fast, e.g., O(1).
AVL trees are Binary Search Trees with the additional property that
the methods maintain a "balanced" property:
For every node in an AVL tree, the heights of its children differ by
at most 1.
For the purpose of this definition (and also the implementation), an
empty child will be considered to be at height -1.
The AVL tree below shows the height of each node.

The children of 600 have heights
0 (left child 550) and
-1 (right child empty).
and these differ by only 1.
For a perfectly balanced binary search tree with N keys we saw
h = O(log(N))
But what about the height of an AVL tree with N
keys?
What is an upper bound for the height of an AVL tree with N
keys?
This can be determined if we can answer the reverse
question:
What is a lower bound for the number of keys in an AVL tree of height
h?
Let N be the minimum number of keys that can be in an AVL tree of
height h.
Fact
2h / 2 < N
But this means
h < 2log(N)
Great! The height of an AVL tree is O(log(N)).
Since the height = O(log(N), this means the get method
is guaranteed to be O(log(N)) for an
AVL tree, even though it isn't perfectly balanced.
The put method first does a
search and then either updates a value or else changes a few links
to attach a new key value pair. Since the height is O(log(N)),
this much would also cost only O(log(N)) for the put method.
However, the put method must also maintain the balance
property. So we have make sure that doesn't add any more than
O(log(N)) additional steps.
Maintaining the AVL Tree property, requires that the insert
includes some code to rebalance portions of the tree if the property
would otherwise be violated.
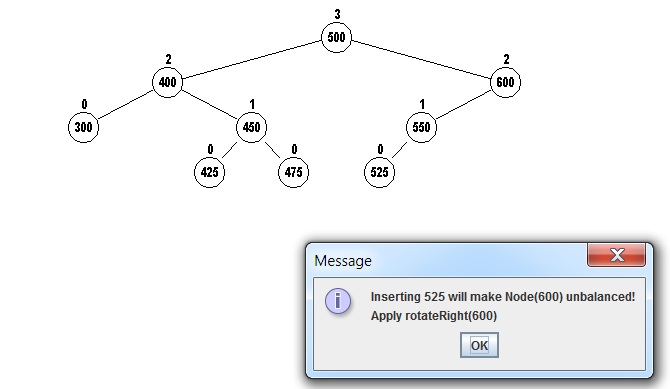
For example if we try to insert the value 525 into this tree in
the usual way as a child of 550, the height of 550 would
become 1, while the right child (empty) of 600 is still at height -1,
a difference of 2.
So the node with 600 would become unbalanced!

This problem is solved by:
1. First insert in the usual way for a binary search tree either in
the left subtree or right subtree. (Duplicates are not allowed in
this version.)
2. Check if the heights of the two children subtrees differs by 2.
If so, then rotate nodes to restore the AVL properties.
Two rotation methods are needed: rotateLeft or rotateRight.
To rebalance an unbalanced node requires we will need to either do one
rotation or two rotations, depending on how the node became unbalanced.
The rotate methods are:
1. private Node rotateLeft( Node p )
2. private Node rotateRight( Node p )
Returning to the example AVL tree, we try to insert 525:
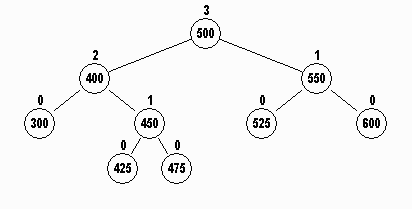
The rotateRight method below is called to rotate the node
p to the right with its
left child, 550 becoming the parent of 525 and 600:
If we try to insert 425 into this tree, node 500 would
then violate the AVL condition. However, we can't use the
rotateRight method:
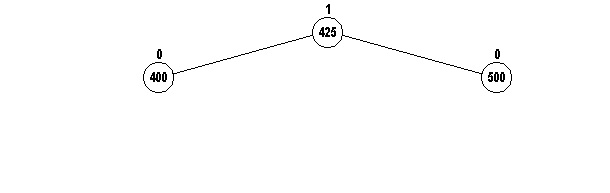
First rotate 400 to the left with its new
right child (425), and then rotate 500 with its new left
child (425 again in a new position) to the right to get:

A slightly more typical example of two rotations is shown
below. The value 450 is being inserted:
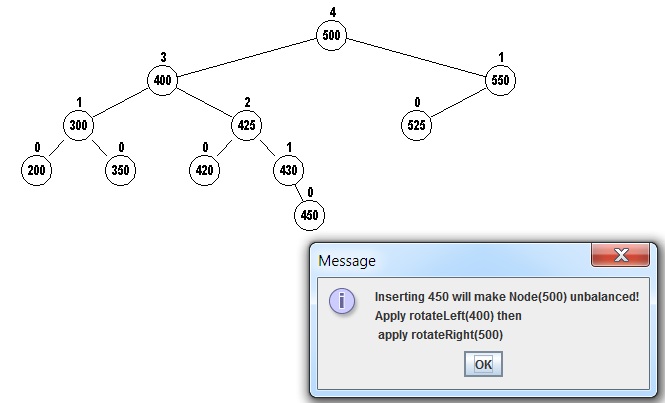
The rotateLeft will rotate 400 to the left, making
425 the new root of the subtree, then rotateRight will
rotate 500 to the right making 425 the new root of the tree.
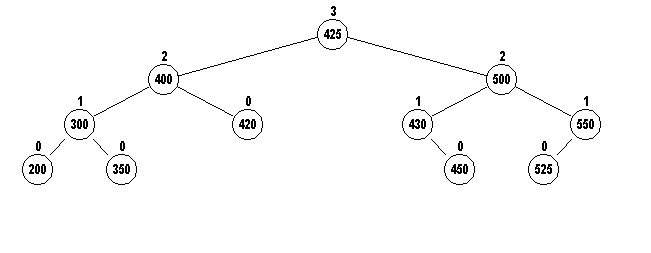
What happened to 425's previous left and right children?
Here is the method:
private static Node rotateLeft( Node p )
{
Node r = ?;
p.right = ?;
r.left = ?;
return r;
}
Note: The height method is a static method that just returns the height of
the node passed to it, but also handles the case if null is
passed. In the later case, height returns -1.
Two rotations are required:
rotateRight Q
rotateLeft P

/*
* item inserted to right of t and left of t.right.
* node t is unbalanced and requires two rotations
*
* 1. rotate t.right to the right and attach the new subtree root to t.right
* 2. rotate t to the left and return the new subtree root
*/
(I'll provide an executable jar file with this demo.)








