• 3.2.2
• 3.2.3
• 3.2.4

The BinarySearchST implementation uses a sorted array of keys which has the advantage of making searches fast - order log(N).

The disadvantage of this array implementation is with insertions.

A binary search tree implementation uses linked nodes, but attempts to retain the advantages of the array implementation while overcoming the disadvantage.

A binary search tree imitates the fast searching possible using binary search in an array by beginning at the root whose key is a value in the "middle".

At the same time, insertion in a binary search tree avoids the disadvantage of having to move other keys as in the array implementation.

A binary search tree implementation of the symbol table type can be more efficient than the array implementation class BinarySearchST.

The value associated with a key plays no role in the implementation of the put, get and delete symbol table methods.

If we omit the value and just keep the key, a symbol table reduces to a collection of distinct keys. But the implementation of the put, get, and delete methods will be the same.

We will examine a binary search tree implementation of such a class, BSTSet, which stores keys only and to simplify things a bit more, we will use only integer keys.

To implement BSTSet as a binary search tree the following private Node inner class will be used:

private class Node
{
  private int key;
  private Node left;
  private Node right;

  private Node(int k)
  {
    key = k;
    left = null;
    right = null;
  }
}

The simple BSTSet will get by with a single data member, the root:

public class BSTSet
{
  private Node root;

  public BSTSet()
  {
    root = null;
  }
  ...
}

If a problem of size N can be broken into subproblems, a method to solve the problem can be implemented by writing and calling methods for each of the subproblems.

If the subproblems are the same as the original problem, but just of smaller size M, then instead of writing different methods for the subproblems, the same method can be use. That is, the method for the original problem can call itself to solve the subproblems. That is, the method can be recursive.

The "problems" for the BSTSet are put, get, and delete. Can these methods be recursive? Why should they be?

The reason they can be recursive is because of the recursive nature of the binary tree itself:

A binary search tree is either:

• empty, or
• a left subtree, a root, a right subtree

For example, to put a key into a non-empty tree, reduces to a subproblem: put the key into the appropriate subtree. So the subproblem is the same as the original problem. Put a key an a binary search tree.

There is a problem with making put recursive. The subtrees, like the whole tree is referenced by the Node at its root. But Node is private in the BSTSet as usual in order to keep a clean separation between the symbol table operations and the implementation.

The solution is to use two methods, one public that doesn't expose the Node type, but which calls a private helper.

The helper method can have Node as a parameter and/or return type since it is private. So it is the helper method that can be recursive.

This approach is often required for other Java classes whenever a recursive method is a natural way to implement a member method.

The size method illustrates the technique.

The size of the tree can be split into subproblems of the same kind:

 size of tree = size of left subtree + size of right subtree + 1 (for the root)
    

Java allows methods to be overloaded, which means that methods in the same class can have the same name. However, they must have different parameter lists. That allows the compiler to know which one is called.

In particular, the public and its private recursive helper can have the same name.

The public size method simply invokes the private, recursive method.

The private recursive size method follows the outline of breaking it into the subproblems of getting the size of the subtrees.

 public int size()
 {
   return size(root);
 }

 private int size(Node t)
 {
   if (t == null) {
     return 0;
   }
   return size(t.left) + size(t.right) + 1;
 }

A public method for drawing the BSTSet trees will be provided. Although it isn't necessary for applications, it may be useful for debugging.

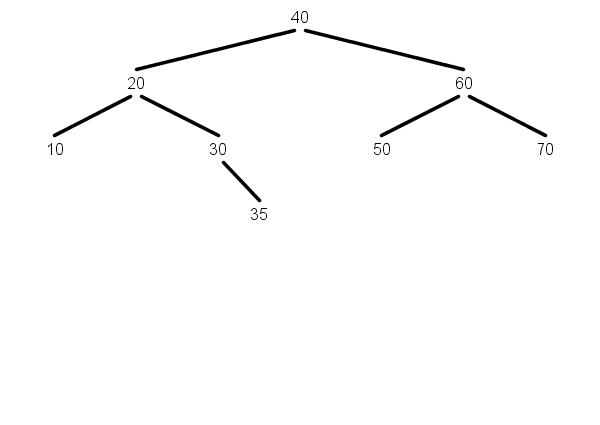
For example,

      BSTSet s = BSTSet.fromString("40 60 70 50 20 10 30 35");
      s.drawTree();
      StdDraw.show();
    

The put method is a slightly different pattern since it changes the tree while the size method does not. This means that put must change some links.

However, put uses the same approach of using a public method and a private, recursive helper method.

The recursive solution the "problem" of putting x into the whole tree reduces to putting x into the appropriate subtree:

if x < root.key, put x in the left subtree
else if x > root.key, put x in the right subtree

The difference between the recursive implementation of size and that of put, is that the private recursive method needs to return a reference to the modified subtree. This return Node is needed since new keys are inserted where a null link was. This null link needs to be reset to reference the Node returned by the recursive call.

The implementation:

public void put(int x)
{
  root = put(root, x);
}

private Node put(Node t, int x)
{
  if (t == null) {
    return new Node(x);
  }
  if (x < t.key) {
     t.left = put(t.left, x);
  } else if (x > t.key) {
     t.right = put(t.right, x);
  }
  return t;
}

The recursive description of the get method to search for x:

 if x < root.key search for x in the left subtree
 else if x > root.key search for x in the right subtree
 else x is found at the root.
    

The delete method follows the public/private recursive general pattern, but as is sometimes the case with data structure classes, the delete method seems to present some additional difficulties.

The delete method for BSTSet is no exception. There are two cases:

• Case 1: The node to be deleted has at most 1 child.

• Case 2: The node to be deleted has 2 children.

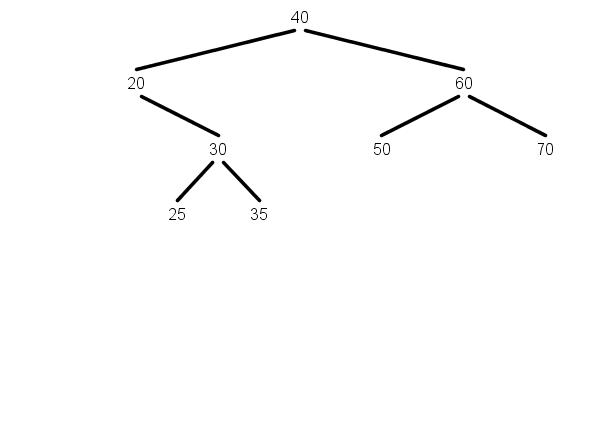
Deletion is easy. In this case the node to be deleted is the root of a subtree, but one link (left or right) is null. Just "promote" the other child to be the new root of the subtree.

The Node with key = 20 below has only one child, 30. To delete 20, "promote" the subtree at 30 to take 20's place as the child of 40.

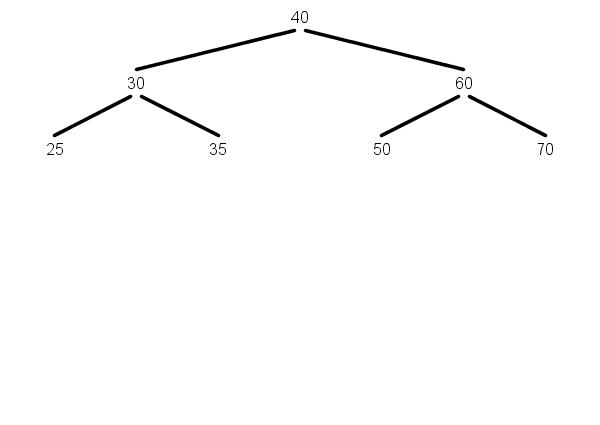
After deleting 20, the subtree at 30 "moves up":

The method to delete a key k can be described easily and is similar to the put method in that we must first find the node containing k (if there is one):

To delete k from the tree:

1. if k < the key in the root of this tree, delete k (recursively) from the left subtree and reattach the modified left subtree.
2. else if k > the key in the root of this tree, delete k from the right subtree and reattach the modified right subtree.
3. else k is equal to the key in the root of the tree. If so, delete this node and return the possibly new root of the modified tree.

This guides us to write the same sort of pair public/private methods for delete as for put, but must fill in the part to delete the Node containing k once we have found it.

We haven't handled the bad case 2 yet, but let's see what the code would be just to handle the search AND case 1.

Begin with the usual public/private pair of methods, remembering that deletion modifies the tree (like put, but unlike size()). In particular the root might change.

public void delete(int k)
{
  root = delete(root, k);
}

public Node delete(Node t, int k)
{
  if (t == null) {
     return null;  // k not in the tree
  }
  // Find the node to delete: the one containing k
  if (k < t.key) {
     t.left = delete(t.left, k);
  } else if (k > t.key) {
    t.right = delete(t.right, k);
  } else { // we found it. Now delete t
    if (t.left == null) { // So we are in case 1
       return t.right;
    } else if (t.right == null) { // Also in case 1
       return t.left;
    } else {
      // THE BAD CASE 2 - t has two children
    }
  }
  return t;
}

If the node to be deleted has 2 children there are 2 obvious candidates to replace the key at that node:

• the next larger key
• the previous smaller key

Once this choice is made, we must decide how to change the tree to accomplish this replacement.

The following choices describe the deletion and is called Hibbard deletion.

• Choose the next larger key as the replacement
• Replace the key to be deleted with this next larger key.
• Delete the replacement key from the subtree where it was located.

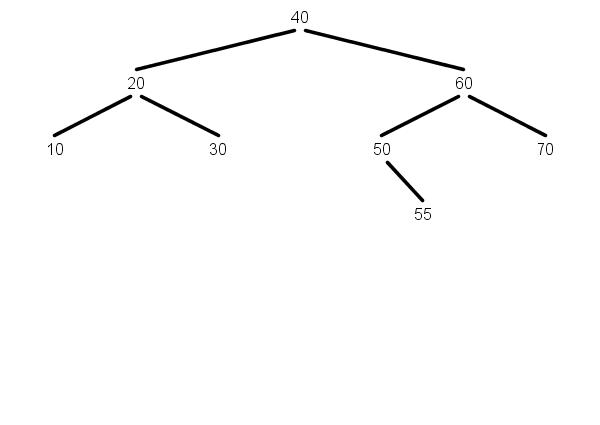
Delete 40 from this tree. The next larger key is 50.

Replace key 40 with 50.

Now 50 is in two nodes. Delete 50 from the right subtree. Note that it in the right subtree 50 will not have a left child, so deleting it is handled by the simpler case 1 part of the code.

Set 50's left and right links to be 40's left child and the modified right child (50 was deleted from the right child).

public void delete(int k)
{
  root = delete(root, k);
}

public Node delete(Node t, int k)
{
  if (t == null) {
     return null;  // k not in the tree
  }
  // Find the node to delete: the one containing k
  if (k < t.key) {
     t.left = delete(t.left, k);
  } else if (k > t.key) {
    t.right = delete(t.right, k);
  } else { // we found it. Now delete t
    if (t.left == null) { // So we are in case 1
       return t.right;
    } else if (t.right == null) { // Also in case 1
       return t.left;
    } else {
      // THE BAD CASE 2 - t has two children
      Node s = min(t.right);
      t.key = s.key;
      t.right = delete(t.right, t.key);
    }
  }
  return t;
}

How would we write min and max?

These follow the pattern of size, and can also be written as the same public/private pair and use recursion.

The binary search tree requires that the keys be ordered. The basic types (int, double, char, ...) have a natural ordering and we use the relational operators <, >, etc.

Class types used as keys must implement the compareTo method, such as String.

So the binary search tree implementations of symbol table (and set) should implement the additional methods for ordered symbol tables:

• min
• max
• floor
• ceiling
• rank
• select

Implementing min and max is easy with the usual approach. What about the others?

This assignment is to add a number of methods to the BSTSet class to give you practice using recursion. The methods will all use the technique of the public/private pair of methods with the private method being the recursive one.

Group I

• size (provided for you)
• height
• sizeOdd - number of Nodes with an odd key
• isPerfectlyBalancedS - at each Node, do left and right subtrees have same size?
• isPerfectlyBalancedH - at each Node, do left and right subtrees have same height?
• isOddBalanced - at each Node, do left and right subtrees contain the same number of odd keys?
• isSemiBalancedI - is each Node semibalanced? leaf or else size(larger child) / size (smaller child) <= 2
• sizeAtDepth - number of nodes at a given depth
• sizeAboveDepth - number of nodes whose depth is < a given depth
• sizeBelowDepth - number of nodes whose depth is > a given depth

Group II

• removeOddSubtrees
• removeLeaves
• removeSingles
• removeDepth
• addZeroToSingles
• sizeAtHeight
• sizeAboveHeight
• sizeBelowHeight
• removeHeight