Regression
Regression is very similar to correlation in that it also tries to determine if two or more variables are related to each other.
However, regression analysis goes one step further. It is used to make predictions. In other words, regression allows us to predict how specific changes in one variable will be related to changes in another variable.
Goal: To predict how a change in one variable is related to a change in another variable.
For example:
How is the number of cigarettes you smoke related to how long you will live? In particular, what is the relationship between each cigarette you smoke and how long you will live? How many minutes does smoking each cigarette take off your life?
Logic Behind Simple Linear Regression.
1. Regression is based on the idea that a line (called a regression line or line of best fit) can be drawn through a scatter plot of two variables.
For example:
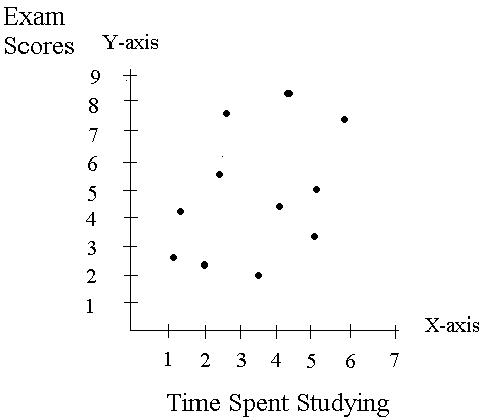
Scatter plot of Time Spent Studying and Exam Scores.

Goal is to draw a line through these data points that best represent the points.
Obviously several different lines could be drawn through this data.
But when doing a regression analysis the regression line is estimated so that it minimizes the distance between the line and all of the points. That is why regression is often called line of best fit.
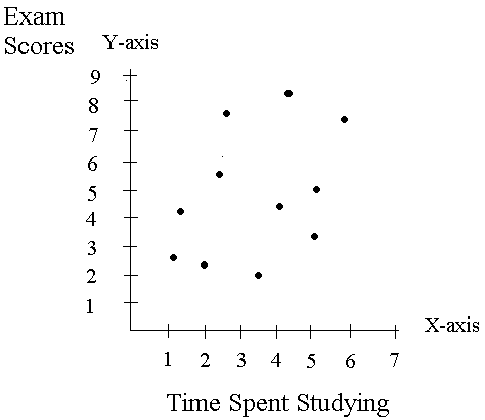
Regression analysis estimates where line should be drawn that best fits the data.
Terms:
Variable on Y-axis is called dependent variable - the variable you are trying to predict.
The variable you are trying to predict.
Variable on the X-axis is called independent variable.
These are variables you think will allow you to make predictions about other variables.
2. Regression line provides two important pieces of information.
a. The Y-intercept .
Where line crosses the Y-axis when X = 0.
Often referred to as constant or a.
b. The slope of the line.
Refers to how slanted the line is.
Rise over run.
Often referred to as beta value or b.
Examples:
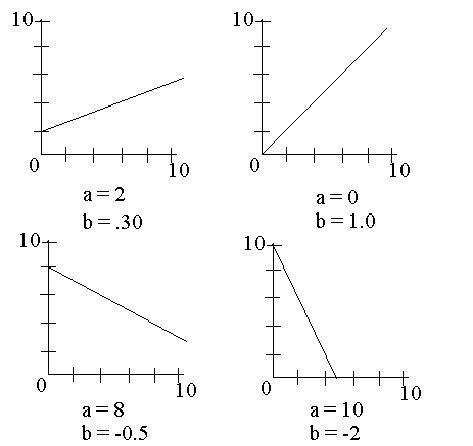
3. The results of a regression analysis can be written in the form of the equation of a line.
Y = a + b(X)
Y is the value on the Y axis (value of dependent variable)
a is the constant or Y - intercept
b is the slope of the line
X refers to the variable on the X-axis (independent variable)
So, lets go back to our original example, now with regression line drawn in.
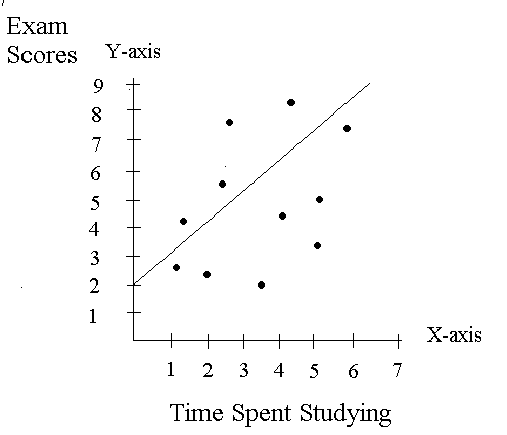
- the constant or y-intercept is 2.
- the beta value or slope is 1
So the equation for our line is
Y = a + b(X)
Or
Exam score = 2 + 1*Time Spent Studying.
So, if you spent zero hours studying, based upon this equation you could expect to get an exam score of 2. (2 + 1*0)
However, if you spent 3 hours studying, you could expect to get an exam score of 5 (2 + 1*3).
As you can see doing an regression analysis can be very useful. Can allow you to make predictions.
4. Can also determine if prediction (slope) is significant (not due to chance) and more importantly, how accurate the prediction is.
a. The further the slope moves away from zero, the more likely that the prediction is not due to chance.
Several ways to determine whether or not slope is significant or not.
Don't need to know these tests
But, do need to know that if slope for a given independent variable is NOT significant, then it does NOT explain change in the dependent variable.
For example, if the slope of time spent studying were not significant, then you would know that time spent studying did not explain or predict how you would do on the exam.
b. How accurate or good a regression line is can be calculated.
r2 indicates the percentage of change in the dependent variable that is explained or accounted for by the regression line.
Lets go back to our regression line.
Exam score = 2 + 1*Time Spent Studying.
If the r2 value of this line were .30 then:
30% of your exam score is explained by this regression line
The time you spend studying explains 30% of your exam score.
If the r2 value of this line were .60 then:
60% of your exam score is explained by this regression line
The time you spend studying, explains 60% of your exam score.
Visually, this is what it would look like.
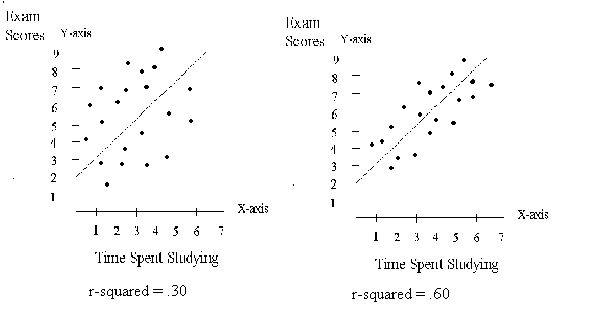
Summary of Simple Linear Regression
1. Trying to find a line that fits the data.
2. Regression line allows you to predict how changes in independent variable will influence changes in dependent variable.
3. r2 tells you the percentage of change in the dependent variable that is explained by the regression line.
Multiple Linear Regression
Goal: To determine how changes in several independent variables are related to a change in the dependent variable.
Logic behind Multiple Linear Regression:
1. Same as linear regression, one dependent variable, but:
a. More than one independent variable.
Say I want to know how intelligence and time spend studying will predict your exam performance.
b. Regression line changes to reflect additional slopes for each independent variable.
Y = a + b1 + b2 + .....
Or
Exam score = a + b1(time spent studying) + b2(intelligence)
c. Accuracy of prediction is now symbolized by R2
Example: (dated but easy to understand)
1. Trying to identify the factors influence how much time women spend per year on housework.
Dependent variable: Time spent doing house work per year (measured in hours).
Independent variables: 9 independent variables were regressed on time spent doing house work.
Four variables were significant predictors of how much time women spend doing housework.
| Independent variables | b |
| Constant | 1,669 |
| Wife's education (in years) | -53 |
| Husband's education (in years) | 22 |
| Number of Children between ages 0 to 17 | 327 |
| Number of rooms in house | 83 |
So regression equation is as follows.
Hours spent cleaning = 1,669 - 53*Wife's education + 22*Husband's education + 327*number of children + 83*number of rooms in house.