Brief Summary of z-tests
Goal: Trying to determine how likely it is that two groups are similar to each other by testing the null hypothesis (no real difference between groups -- control and experimental group are not different from each other)
How: Create a distribution of differences. Take all possible combinations of samples from the entire population and calculate all of the possible distances between every pair of possible samples. Plot all of these possible differences.

The mean of this distribution (m diff = 0).
The standard deviation of this distribution can be calculated (s diff) which tells you how spread out all of the scores are.
Use this distribution to find out exactly how likely or probable it was to get the type of difference observed between the two samples used in the experiment (control and experimental groups).
A z-score can be calculated for the difference observed between the control and experimental group.
z = (distance between groups - m diff )/ s diff
The z-score simply tells you where the difference between the two groups you observed falls in relation to all of the possible differences that could occur.
If the distance between the two groups is not that unusual (it is very common), then say that the groups are equal to each other (accept the null hypothesis).
If the distance between the two groups is not very common, then reject the null hypothesis and assume that the groups are different from each other. In other words, the difference between the two groups is not due to chance, but the difference is due to the variable that was manipulated during the experiment.
To determine whether or not a given difference is very common or unusual, social scientists typically use a cut off level, called the probability or significance level.
To be considered unusual, the difference observed must occur, at least, less than 5 times out of a hundred (p < .05).
Non-directional tests of significance or Two-tailed tests
For a non-directional test the following information is used to determine whether or not the difference observed was likely to occur less than 5 times out of hundred (p < .05).
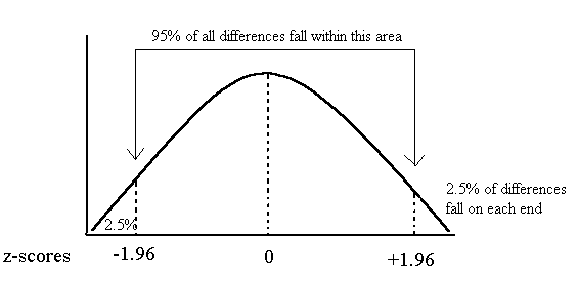
So, if the z-score you obtained is less than -1.96 or greater than +1.96 then you know the distance between the two groups is unusual (likely to happen only 5 out of a hundred times). So, you reject the null hypothesis and assume the groups are truly different from each other. Differences not due to chance.
-1.96 and +1.96 are called critical values. Anything beyond these values is unusual - not likely to happen.
You can also check whether or not the difference obtained is even less likely to have occurred. Typically researchers also check to see whether the null hypothesis can be rejected at p < .01. Odds are less than 1 in a hundred of getting this big of a difference.
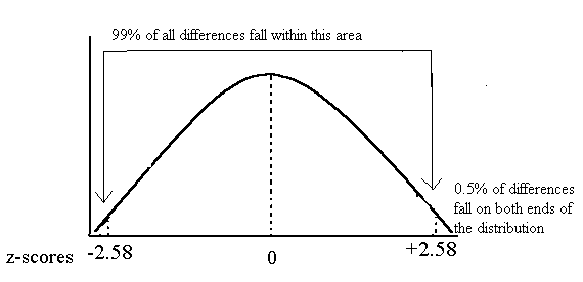
In this case, if the z-score you obtained is less than -2.58 or greater than +2.58 then you know the distance between the two groups is very unusual (only likely to happen 1 out of a hundred times). So, you reject the null hypothesis and assume the groups are truly different from each other. Differences not due to chance.
Critical values are -2.58 and +2.58 in this case.
Directional tests of significance or One-Tailed tests
For a directional test you first must determine whether the z-score obtained is in the correct direction. So, if you predict that group #1 will be larger than group #2 then you must have a positive z-score. If the z-score is negative, you simply accept the null hypothesis.
If the z-score is in the correct direction, then use the following information to determine whether or not the difference observed was likely to occur at a p < .05 and p < .01 significance level.
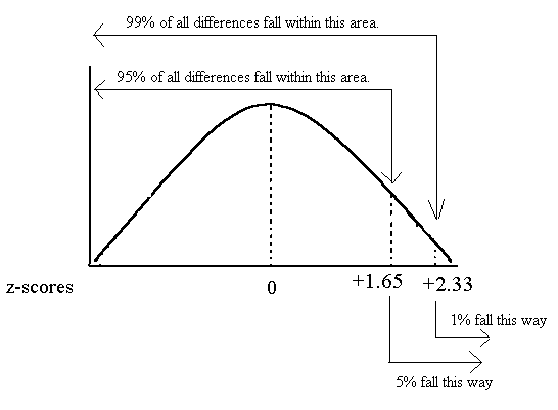
So, when checking for a positive difference, if a z-score is greater than +1.65 then we reject the null at (p <. 05) and if a z-score is greater than +2.33 then we reject the null at (p < .01).
Critical values are +1.65 and +2.33.
If checking whether the first group is smaller than second group, then check only the negative end of the distribution.
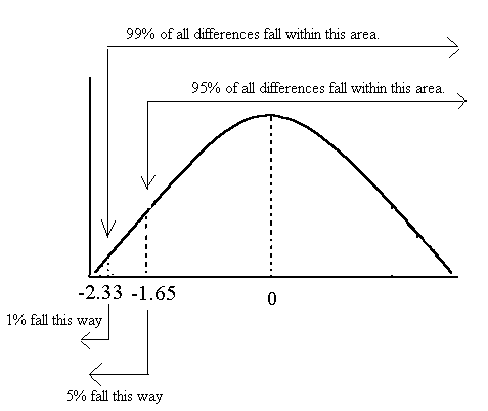
So, when checking for a negative difference, if a z-score is less than -1.65 then we reject the null at (p <. 05) and if a z-score is less than -2.33 then we reject the null at (p < .01).
Critical values are -1.65 and -2.33