To Documents

Histograms

The Histogram

• Here are the directions for drawing a histogram:
  1. Divide an interval containing the data into equally spaced intervals called bins. Except for the last interval, each interval is closed on the left and open on the right.

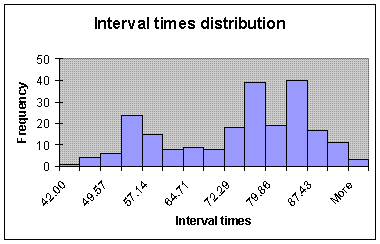
     Example:   If the data is

     5  39  75  79  85  90  91  93  93  98,

     divide the interval [0,100] into the five bins
     [0,20)  [20,40)  [40,60)  [60,80)  [80,100].

  2. Prepare a table listing the number of observations (frequency) in each bin:

     Example:

     Bin	Frequency
     [0,20)	1
     [20,40)	1
     [40,60)	0
     [60,80)	2
     [80,100)	5

  3. Draw a histogram with one rectangle for each bin. The base of each rectangle coincides with its bin. The height of each rectangle is the frequency of that bin.

     Example:   Here is the histogram drawn from the table in Step 3.

Bell-shaped Histograms

• Many histograms of real data are bell shaped. Here is the standard bell-shaped curve:

  

• Notice that the bell-shaped curve is symmetric around its center.

• If a histogram is bell shaped, it can be parsimoniously described by its center and spread.
  The center is the location of its axis of symmetry.

  The spread is the distance between the center and one of its inflection points.

• Here is the histogram of some times between eruptions of the Old Faithful Geyser in minutes:

  

• This histogram is not bell-shaped, so the center and spread are not a good summary of the data.