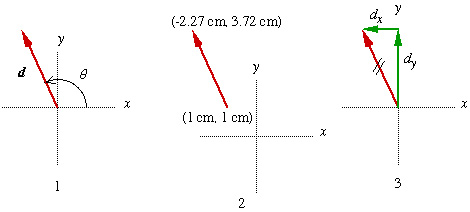
I. You can describe a vector, for our purposes, in three ways, as illustrated below.

1. Describe by giving magnitude (number and unit) and direction (angle measured counterclockwise from +x axis).
    Here, d = 3 cm at 115^o. (Note: The "tail" of the vector need not be located at the origin.)

2.  Describe by giving the x and y coordinates of the "head" and "tail" of the vector.

3.  Describe by giving the components of the vector. Here:

    d_x = dcosq = (3 cm)(cos115^o) = -1.27 cm      d_y = dsinq = (3 cm)(sin115^o) = 2.72 cm
    (d is the magnitude, i.e., absolute value, of the vector d.)
    For clarity in a vector diagram, two lines are drawn through a vector when it is replaced by its components.

II. The negative of a vector has the same magnitude as the original vector, but the direction angle is rotated 180^o.
     In the example illustrated above,  - d = 3 cm at 295^o.

III. Vector addition.

1. To add two or more vectors graphically, use the "head-to-tail" method. Measure the sum (also called the resultant)
    with ruler and protractor.

2.  To add two or more vectors analytically,
     (a) calculate the components of each vector,
     (b) find the sums of the x and y components,
     (c) use the Pythagorean theorem to find the magnitude of the resultant (sum),
     (d) use the inverse tangent function to find the direction angle of the resultant.

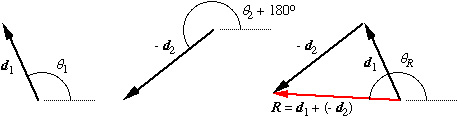
     Example. Find the sum of d₁ = 3 cm at 115^o, d₂ = 4 cm at 38^o, d₃ = 3 cm at 180^o.

     The three vectors are drawn below, along with the vector sum. You can see that the resultant R can be obtained
     by adding the vectors in any order: d₁ + d₂ + d₃ = d₃ + d₁ + d₂ . Vector addition is commutative.
 



The careful use of ruler and protractor should give:  R = 5.30 cm at 102^o.

The sum is calculated. It is a good idea to carry an extra significant figure.

d_1x = 3cos115^o = -1.268         d_1y = 3sin115^o= 2.719
d_2x = 5cos38^o   = 3.152          d_2y = 5sin38^o  = 2.463
d_3x = 3cos180^o = -3               d_3y = 3sin180^o = 0
          R_x = Sd_x= -1.116 cm            R_y = Sd_y= 5.182 cm

R = [(-1.116 cm)² + (5.182 cm)²]^1/2 = 5.30 cm
q_R = tan^-1(5.182/-1.116) = 102^o

IV. Vector subtraction

     Subtracting d₂ from d₁ is the same as adding d₁ and -d₂.



    d_1x = 3cos115^o = -1.268                d_1y = 3sin115^o= 2.719
- d_2x = 4cos218^o   = - 3.152          - d_2y = 4sin218^o  = - 2.463
                      R_x = - 4.420                                 R_y = 0.256

R = 4.43 cm at 177^o

If the resultant is not in the first quadrant, as in this example, the following procedure may be used to find the angle of the resultant vector.

1. Find the inverse tangent of the absolute values of the components: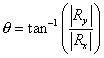 

2. Find the angle of the resultant, q_R, as indicated on this table.
 

Quadrant	x-component	y-component	qR
I	+	-	qR = q
II	-	+	qR = 180o - q
III	-	-	qR = 180o + q
IV	+	-	qR = 360o - q


 
In the subtraction example above, the x-component is negative and the y-component is positive. The vector lies in the second quadrant.

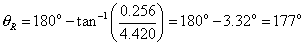
INVERSE TRIG FUNCTIONS ON THE CALCULATOR

If you set your calculator to degrees and ask it to find the inverse sine of0 .5, that is to find the angle whose sine is 0.5, your calculator should display 30^o. That is, the angle whose sine is 0.5 is 30^o. Now ask it to find sin(180^o –30^o). You can see that the sin(150^o) is also 0.5. Apparently, your calculator “knows” how to calculate the sine of an angle greater than 90^o, but will not return a value for the inverse sine greater than 90^o. Now look at sin^-1(-0.5). Your calculator will give you –30^o. Now look at sin(210^o) and sin(330^o). The sines of these angles are also -0.5. It looks like your calculator will always return inverse sine values between –90^o and 90^o for any numbers between -1 and 1. Similar problems occur when you look for the inverse cosine and the inverse tangent.

This is a limitation of the calculator you will encounter when working problems involving vectors. Here is an example. Suppose the components of a displacement vector are given as: dx = –3 and dy = –4. If you draw these components you can see that the corresponding vector d has a magnitude of 5 units. You can also see that this vector lies in the third quadrant; the direction angle is between 180o and 270o. However, if you ask your calculator for tan-1(-4/–5) you will see 53.1o, an angle in the first quadrant! The graphs shown below indicate the range of operation (the darker portions of the curves) of a calculator for taking the inverse trig functions. The table in the previous section shows how to change the angle given by your calculator when the vector in question is not in the first quadrant.

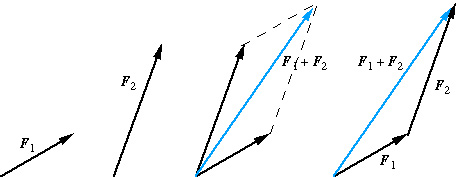
For convenience, to help clarify diagrams, it is allowable to "move" a vector parallel to itself.

Suppose two forces are specified: F₁ = 3 N at 20^o, F₂ = 5 N at 70^o.

The resultant force is R = 7.55 N at 55.2^o. (You should be able to do this calculation.)

The vector diagram, in this case, is clearer if both vectors originate at the point where they are applied.
This is a good way to represent velocities, accelerations or concurrent forces.
The vectors are joined tail-to-tail and the resultant is the diagonal of the paralellogram, as shown here.
You can see that the two methods are equivalent.
 


 



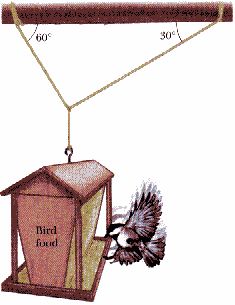
VI. Worked Example - Vector Components and Equilibrium

A bird feeder that weighs 160 N is supported by three cables, as shown here. Calculate the tension in each cable.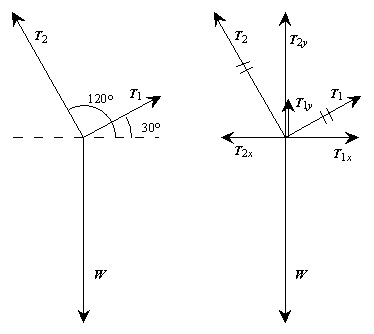

 

Return