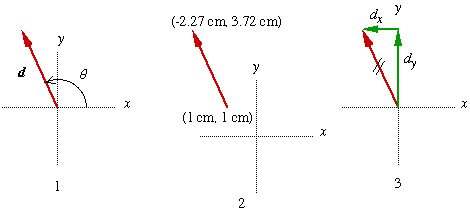
I. You can describe a vector, for our purposes, in three ways, as illustrated below.

1. Describe by giving magnitude (number and unit) and direction (angle measured counterclockwise from +x axis).
    Here, d = 3 cm at 115^o. (Note: The "tail" of the vector need not be located at the origin.)

2.  Describe by giving the x and y coordinates of the "head" and "tail" of the vector.

3.  Describe by giving the components of the vector. Here:

    d_x = dcosq = (3 cm)(cos115^o) = -1.27 cm      d_y = dsinq = (3 cm)(sin115^o) = 2.72 cm
    (d is the magnitude, i.e., absolute value, of the vector d.)
    For clarity in a vector diagram, two lines are drawn through a vector when it is replaced by its components.

II. The negative of a vector has the same magnitude as the original vector, but the direction angle is rotated 180^o.
     In the example illustrated above,  - d = 3 cm at 295^o.

III. Vector addition.

1. To add two or more vectors graphically, use the "head-to-tail" method. Measure the sum (also called the resultant)
    with ruler and protractor.

2.  To add two or more vectors analytically,
     (a) calculate the components of each vector,
     (b) find the sums of the x and y components,
     (c) use the Pythagorean theorem to find the magnitude of the resultant (sum),
     (d) use the inverse tangent function to find the direction angle of the resultant.

     Example. Find the sum of d₁ = 3 cm at 115^o, d₂ = 4 cm at 38^o, d₃ = 3 cm at 180^o.

     The three vectors are drawn below, along with the vector sum. You can see that the resultant R can be obtained
     by adding the vectors in any order: d₁ + d₂ + d₃ = d₃ + d₁ + d₂ . Vector addition is commutative.
 



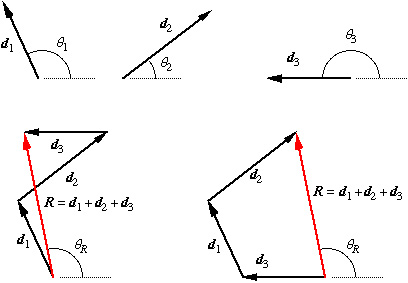
The careful use of ruler and protractor should give:  R = 5.30 cm at 102^o.

The sum is calculated. It is a good idea to carry an extra significant figure.

d_1x = 3cos115^o = -1.268         d_1y = 3sin115^o= 2.719
d_2x = 5cos38^o   = 3.152          d_2y = 5sin38^o  = 2.463
d_3x = 3cos180^o = -3               d_3y = 3sin180^o = 0
          R_x = Sd_x= -1.116 cm            R_y = Sd_y= 5.182 cm

R = [(-1.116 cm)² + (5.182 cm)²]^1/2 = 5.30 cm
q_R = tan^-1(5.182/-1.116) = 102^o

IV. Vector subtraction

     Subtracting d₂ from d₁ is the same as adding d₁ and -d₂.



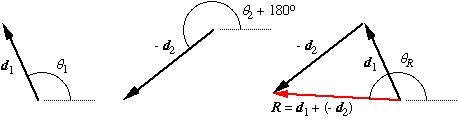
    d_1x = 3cos115^o = -1.268                d_1y = 3sin115^o= 2.719
- d_2x = 4cos218^o   = - 3.152          - d_2y = 4sin218^o  = - 2.463
                      R_x = - 4.420                                 R_y = 0.256

R = 4.43 cm at 177^o

If the resultant is not in the first quadrant, as in this example, the following procedure may be used to find the angle of the result

1. Find the inverse tangent of the absolute values of the components: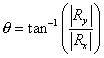

2. Find the angle of the resultant, q_R, as indicated on this table.
 

Quadrant	x-component	y-component	qR
I	+	-	qR = q
II	-	+	qR = 180o - q
III	-	-	qR = 180o + q
IV	+	-	qR = 360o - q

In the subtraction example above, the x-component is negative and the y-component is positive. The vector lies in the second quadrant.

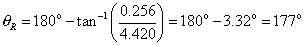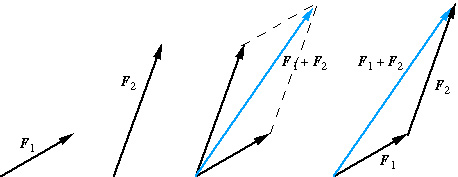
Suppose two forces are specified: F₁ = 3 N at 20^o, F₂ = 5 N at 70^o.

The resultant force is R = 7.55 N at 55.2^o. (You should be able to do this calculation.)

The vector diagram, in this case, is clearer if both vectors originate at the point where they are applied.
This is a good way to represent velocities, accelerations or concurrent forces.
The vectors are joined tail-to-tail and the resultant is the diagonal of the paralellogram, as shown here.
You can see that the two methods are equivalent.
 


 
 

Return