Binary Search Trees have worst case performance for the symbol table operations - put and get - the same as for a linked list.

To guarantee these operations have order of growth log(N), we need to keep the trees balanced.

Keeping the tree balanced guarantees that the paths have length proportional to log(N).

Both put and get must traverse one path and so traversing a path will cost at most log(N) operations.

But we have to add to this the cost of rebalancing.

So the cost of keeping the tree balanced must be small so that the order of growth of put and get remains log(N).

What does it mean for a BST to be balanced?

There are several possibilities that all lead to all paths in the tree having length at most proportional to log(N).

Two different kinds of balanced BSTs using slightly different definitions of balanced are:

• AVL tree
• Red Black tree

AVL trees are Binary Search Trees with the additional property that the methods maintain a "balanced" property:

      For every node in an AVL tree, the heights of its children differ by
      at most 1.
    

For the purpose of this definition (and also the implementation), an empty child will be considered to be at height -1.

The AVL tree below shows the height of each node.

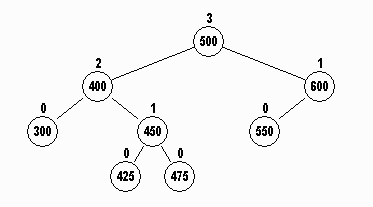
      The children of 600 have heights 

       0 (left child 550) and
      -1 (right child empty).

      and these differ by only 1.
    

What is the an upper bound for the height of an AVL tree with N nodes?

This can be determined if we can answer the reverse question:

What is a lower bound for the number of nodes in an AVL tree of height h?

Let f(h) be the minimum number of nodes that can be in an AVL tree of height h.

Then

      f(-1) = 0
      f(0) = 1
      f(1) = 2
    

For h >= 1,

      f(h) = 1 + f(h-1) + f(h-2)
    

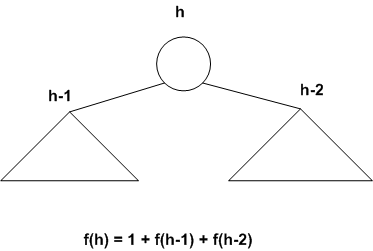
Since f(h-1) >= f(h-2), we get

      f(h) > 2f(h-2)   (for all h >= 1)
    

f(7) > 2f(5)	f(8) > 2f(6)
f(7) > 22f(3)	f(8) > 22f(4)
f(7) > 23f(1)	f(8) > 23f(2)
f(7) > 232	f(8) > 24f(0)
f(7) > 24	f(8) > 24

In general,

      f(h) > 2ceiling(h/2) > 2h/2
    

where ceiling(x) means the smallest integer that is >= x.

Let h be the maximum height for an AVL tree with N nodes. Then f(h) must be <= N.

  2h/2 < f(h) <= N

Taking log₂ we get

      h/2 < log2(N)

      or

      h < 2log2(N)


    

So the height of an AVL tree with N nodes is O(log(N)).

Maintaining the AVL Tree property, requires that the insert includes some code to rebalance portions of the tree if the property would otherwise be violated.

For example if we try to insert the value 525 into this tree in the usual way as a child of 550, the height of 550 would become 1, while the right child (empty) of 600 is still at height -1, a difference of 2.

So the node with 600 would become unbalanced!

This problem is solved by:

      1. First insert in the usual way for a binary search tree either in
      the left subtree or right subtree. (Duplicates are not allowed in
      this version.)
      2. Check if the heights of the two children subtrees differs by 2.
      If so, then rotate nodes to restore the AVL properties.
    

Returning to the example AVL tree, we try to insert 190:

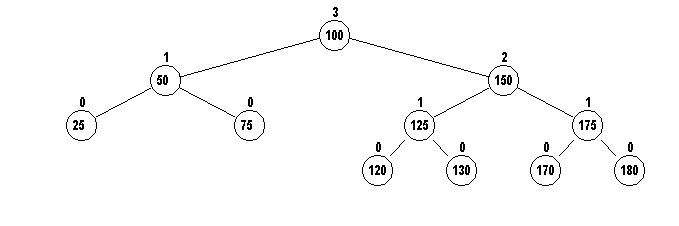
The rotateLeft(Node t) method is called where t is the unbalanced Node (100 in this example) to rotate the t and its right child to the left.

The result is

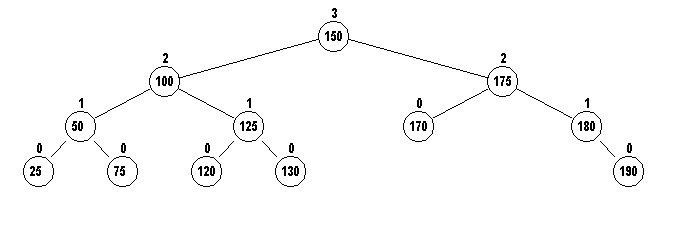
What happened? How many links were changed?

What is the code for void rotateLeft(Node t)?

      
                 100 [h=3]
                /   \
               /     \
      [h=1]   A      150 [h=2]
                    /   \
                   /     \
            [h=1] B       C [h=1]
    

Inserting 190 will make subtree C at 175 have height 2 with children of height 0 and 1
(175 will still be balanced).

This makes the subtree at 150 height 3 with children of height 1 and 2
(150 will still be balanced)

But this makes the subtree at 100 unbalanced. Its children will have heights 1 and 3
(100 will be unbalanced)!

      
           100 [h=3]                                           150 [h=3] 
          /   \                                               /   \                              
         /     \                                             /     \                             
  [h=1] A      150 [h=2 -> 3]            =>           [h=2] 100     C [h=2]  
              /   \                                        /   \                         
             /     \                                      /     \                        
      [h=1] B       C [h=1 -> 2]                   [h=1] A       B [h=1]
    

Here is the method:

  private Node rotateLeft( Node t )
  {
    // Rotate left with p's right child
    Node r = ?;
    t.right = ?;
    r.left = ?;

    // Adjust the heights since the nodes have been rotated.
    t.height = Math.max( height(p.left), height(p.right) ) + 1;
    r.height = Math.max( height(r.left), height(r.right) ) + 1;

    return r;
  }

Note: The height method just returns the height of
the node passed to it, but also handles the case if null is
passed. In the later case, height returns -1.