Definition

The log of N to the base b is the exponent a such that

      N = ba
    

and is written

      logb(N) = a
    

For example,

      1000 = 103,  so log10(1000) = 3

      1024 = 210,  so log2(1024) = 10
    

Logarithms with different Bases

Log to the base 2 is just a constant multiple of the log to the base 10.

Log to base 2 is a (different) constant multiple of the log to any other base b, where the constant depends only on the two bases.

      log2(N) = log10(N) / log10(2)
    

For example, what if N is 2?

Since logarithms of different bases differ only by a constant depending only on the bases, the base will be omitted and assumed to be 2 unless otherwise noted.

The basic property of logarithm function (for any base):

 log(xy) = log(x) + log(y)
    

      For 
      x = 2a,   log(x) = a
      y = 2b,   log(y) = b

      xy = 2a + b
    

So

      log(xy) = a + b = log(x) + log(y)
    

 (1) log(2N) = log(N) + 1

 (2) log(N2) = 2log(N)

 (3) log(N100) = 100log(N)

 (4) log(N0.5) = 0.5log(N)
    

Since

      2N + 1 ~ 2N
    

this can be combined with the logarithm and then use the log properties to get a tilde approximation for

      log(2N + 1) ~ log(N)
    

like this:

(1) log(2N + 1) ~ log(2N) 

(2) log(2N) = log(2) + log(N) = 1 + log(N)

(3) 1 + log(N) ~ log(N)
    

O(...) means "order of growth ...

Arithmetic Sum

(1)   1 + 2 + 3 + 4 + ... + N = 0.5N2 + 0.5N 
                              ~ 0.5N2
                              = O(N2)
    

Geometric Sum

For N a power of 2: N = 2^k

(2) 1 + 2 + 4 + 8 + ... + N = 2N - 1
                            ~ 2N
                            = O(N)
    

Suggested steps

1. Decide on an input model; that is, what will be used as the input size.
2. Identify the inner loop; that is, the part of the code that will execute most often and/or contribute most to the running time.
3. Decide on a cost model; that is what operations in the inner loop are to be counted.
4. Determine the the total count of the operations in the cost model for a given input size.

The input model in the following examples will just use the input size as the value of N.

The cost model will be to body of the inner for loop (or the single for loop if there is no nested loop). The only operation to count in the inner loop is the single statement:

 sum++;      
    

That is, this will count as 1 operation.

This model seems to make many simplifications, but as seen previously it likely will yield the same tilde approximation and order of growth as a more detailed model.

      // Example 1 O(N)
    for(int i = 0; i < N; i++) {
      sum++;
    }

      // Example 2 O(N^2)
    for(int i = 1; i <= N; i++) {
      for(int j = 0; j < N; j++) {
	sum++;
      }
    }

      // Example 3 O(N^2)
    for(int i = 1; i <= N; i++) {
      for(int j = 0; j < i; j++) {
	sum++;
      }
    }

      // Example 4 O(N)
    for(int i = 1; i < N; i *= 2) {
      for(int j = 0; j < i; j++) {
	sum++;
      }
    }

      // Example 5 O( Nlog(N) )
    for(int i = 1; i < N; i *= 2) {
      for(int j = 0; j < N; j++) {
	sum++;
      }
    }

      // Example 6 O( log(N) )
    for(int i = N; i > 1; i /= 2) {
      sum++;
    }

    for(int i = 0; i < N; i++) {
      sum++;
    }
 
    

    for(int i = 1; i <= N; i++) {
      for(int j = 0; j < N; j++) {
	sum++;
      }
    }
 
    

    for(int i = 1; i <= N; i++) {
      for(int j = 0; j < i; j++) {
	sum++;
      }
    }
 
    

Assume N is a power of 2; e.g., N = 2^k

    for(int i = 1; i < N; i *= 2) {
      for(int j = 0; j < i; j++) {
	sum++;
      }
    }
 
    

Assume N is a power of 2; e.g., N = 2^k

    for(int i = 1; i < N; i *= 2) {
      for(int j = 0; j < N; j++) {
	sum++;
      }
    }
 
    

Assume N is a power of 2; e.g., N = 2^k

    for(int i = N; i > 1; i /= 2) {
      sum++;
    }
 
    

A machine executes 1 instruction per microsecond (that is, 1,000,000 instructions per second).

Algorithm k (for k = 1, 2, 3, 4) takes T_k(N) microseconds for input of size N.

What is the largest input size, N, that each algorithm can complete in 1 second?

      T1(N) = log(N)  (base 2)
      T2(N) = N
      T3(N) = N2
      T4(N) = N3
    

private class Node
{
  public E data;  /* E declared in the containing class */
  public Node next;
  public Node prev;

  public Node(E d)
  {
    data = d;
    next = null;
    prev = null;
  }
}

Using doubly linked nodes can solve the problem of removing the last element efficiently.

Using doubly linked nodes does a bit more code to update both next and prev members instead of just next.

But both doubly linked lists as well as singly linked lists have to be careful to handle boundary cases:

• adding an item to an empty list
• removing an item from a list with only one item

One addition to the structure will allow these boundary cases to be handled with the same code as non boundary cases.

The change is to add two guard nodes: one at the beginning before the first data node and the other after the last data node.

This has the benefit that every data node will have a node before it and one after. In particular this is true even for the first data node and for the last data node.

The head and tail nodes below are the guard nodes:

Empty List: size 0

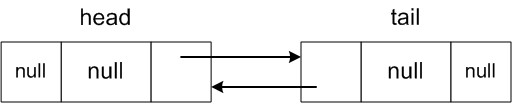
Non-Empty List: size 3

Implement a generic Deque class that implements Iterable.

Deque<E>
-Node head; -Node tail -int sz;
Deque() boolean isEmpty() int size() void pushLeft(E x) void pushRight(E x) E popLeft() E popRight() Iterator<E> iterator()

1. ThreeSum
2. Closest Pair
3. Farthest Pair
4. Autoboxing
5. Estimating the Running time

Implementing a Queue using two Stacks