There is a simple and very useful rule regarding lines tangent to a circle: The radius, which passes through the point of tangency, is always perpendicular to the tangent line.

This rule allows for a variety of methods for constructing tangent lines and tangent arcs.

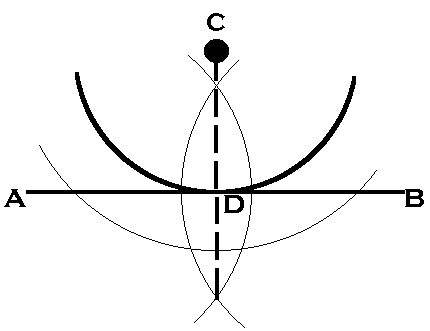
 Arc tangent to a line with the arc center given:

Procedure:With C as the center of the arc and AB to be the tangent line, the first step is to construct a perpendicular from C to AB. If D is the intersection of AB and the perpendicular, then CD becomes the radius of the tangent arc.

 Arc tangent to a point on a line with the Arc radius given:
 

Procedure: Construct a perpendicular from point C on line AB. Set the compass to the radius of the arc and strike this distance from C onto the perpendicular to locate D, the center of the arc. DC is then the radius of the tangent arc.

Line tangent to a point on an arc where the arc center is given:
 

Procedure: Extend a radius from A, the arc center, through B the point of tangency. At B construct CD as the perpendicular to this radius. CD will be tangent to the arc at point B.

Line tangent to a point on an arc of given radius:
 

Procedure: Choose any point C on the arc. Set the compass to the given radius and strike intersecting arcs from B, the point of tangency, and from C. These arcs will cross at the center of the tangent arc. From A draw a radius through B. Construct a perpendicular through the radius at B.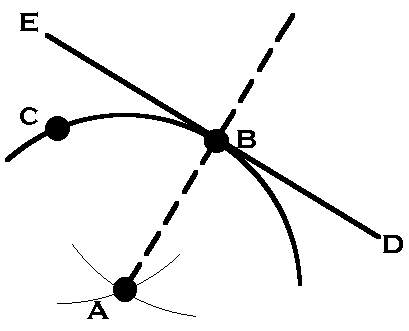

Line tangent to a point on an arc:
 

Procedure: From B, the point of tangency, strike an arc that intersects the tangent arc at A and C. AC then defines a chord, whose ends are equidistant from B. The perpendicular bisector of chord AC will be the radius which passes through B. Line ED is the perpendicular of this radius at B and therefore tangent.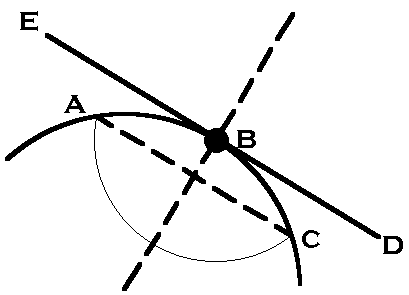

Tangent arcs:

All of the procedures above rely on establishing the radius of the arc through the point of tangency and then constructing a perpendicular to the radius at that point. Constructing two arcs tangent to one another is equally simple.
 

Once the radius of a given arc has been constructed through the point of tangency, all one need do is to extend the radius and locate the center of the tangent arc on that same line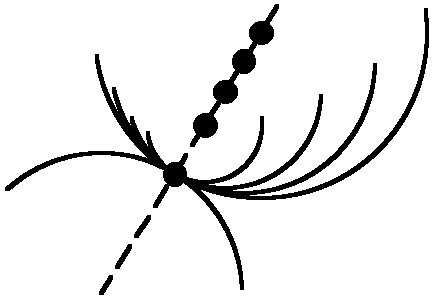

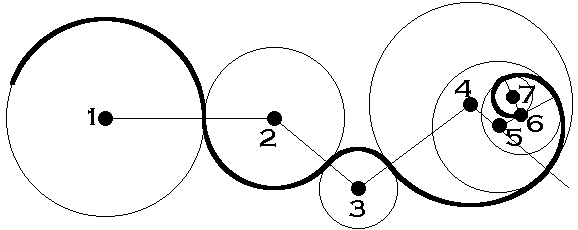
All of the arcs above are tangent to one another. All pass through a common point and all of their centers are situated on the same radial line.

 A series of connected arcs can be used to construct complex continuous curves as long as the successive arcs are tangent: