A unique circle can be defined by 1) a center point and a point on the circle, 2) a diameter and 3) three points on the circle:

Center/point construction:
 

Procedure: Center point A and linear point B are the endpoints of a radius. Set the point of the compass on A and the lead on B and draw the circle.

Diameter construction:
 

Procedure: Bisect diameter AB. Since C denotes the midpoint of AB, then AC and BC are radii of the circle and can either be used to set the compass.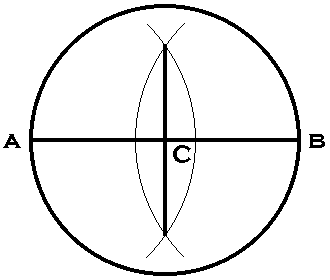

Three-point construction:
 

Procedure: Connect the points A, B and C to form two lines, AB and BC. Construct perpendicular bisectors to both lines and extend these lines so that they intersect. The point of intersection, D, will be the center of the circle.

The method above works because AB and BC are chords and the perpendicular bisectors of chords are always radii. A similar method can be used to locate the center of a circle:
 

Procedure: Draw any two lines BC and AD as chords of the circle. Between the points of intersection of these lines with the circle construct perpendicular bisectors. The intersection of the bisectors, E, will be the center of the circle.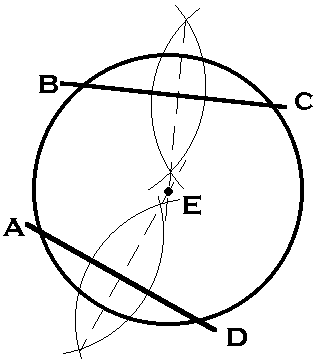