9/21/10 Notes

To Lecture Notes

LSP 121 -- 9/21/10

Review Questions

What does x mean?
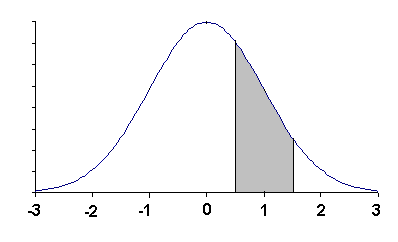
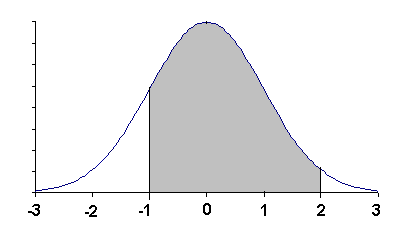
Ans: It means the sample mean = sample average.
What does SD+ mean?
Ans: The sample standard deviation, where you divide by n - 1 instead of n.
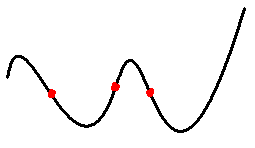
Where are the points marked in red called?

Ans: Inflection points.
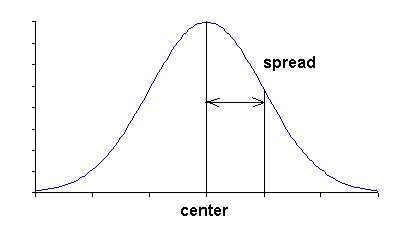
How are inflection points of a normal histogram related to its spread?
Ans: The spread is the horizontal distance between the center of the normal histogram and one of the inflection points.
What are some types of data that are approximately normally distributed.
Ans: Heights, length of hair, finger nails, or claws that have not been cut. Velocities of molecules in an ideal gas, IQ scores.
What two numbers form a good description normally distributed data?
Ans: x and SD+.
How do you compute z-scores?
Ans: z = (x - x) / SD+, Ans: A z-score tells you how many SDs away from the mean you are.
How do you find outliers using z-scores?
Ans: Extreme outliers have a z-score more than 3 or less than -3; mild outliers have a z-score more than 2 or less than -2 and are not extreme outliers.
Note: the outliers found with the boxplot might not be the same as the outliers obtained with the z-scores.

Measures of Variables in SPSS

There three types of measures for variables:
1. Nominal or categorical variables are nonnumeric. Examples are gender, race, occupation, major, breed (for dogs).
2. Scale or continuous variables can take any real value in a range. Examples are age, price, exam score, pressure, temperature.
3. Ordinal variables can take on only whole number values. Examples are college class (1=freshman, 2=sophomore, 3=junior, 4=senior), survey answers (1=strongly disagree, 2=disagree, 3=agree, 4=strongly agree), class grade (A=4, B=3, C=2, D=1, F=0),

Computing z-scores with SPSS

Here are the steps for computing z-scores of the following list with SPSS:
1. Enter the numbers into a column of a new SPSS dataset.
2. Rename the column to x.
3. Change the number of digits after the decimal point to 5 to increase the accuracy of the computed x and SD+.
4. Verify that the measure of the variable is scale.
5. Use Analyze >> Descriptive Statistics >> Descriptives to compute x and SD+ for the data. You should obtain x=58.125 and SD+=26.31912667.
6. Compute the z-scores: on the Data Editor Window, select Transform >> Compute Variable. Enter z in the Target Variable box and (x - 58.125) / 26.31912667 in the Numeric Expression Box. Click OK. A new column named z will appear in the Data Editor Window.
7. To check your result, increase the number of digits after the decimal points to 5 and compute x and SD+ for the z column. You should obtain x=0.0000000 and SD+=0.99999996. Since the mean is 0 and SD+ is 1 for the z-scores, the z-scores are correctly computed.

Areas under a Normal Histogram

If x and SD+ really form a good description of a normal histogram, then given x and SD, we should be able to reconstruct the histogram; that is, we should be able to predict the proportion of observations in any bin of the form (-∞, a], (a, ∞], or [a, b].

We start with the simplest case of a normal histogram with center x = 0 and spread SD+ = 1. Such a histogram is called a standard normal histogram.

Our tool for determining areas under the normal histogram is the standard normal table.
Example 1: What proportion of the observations are in this bin: (-∞, -1.00]?

Solution: The value -1.00 on the x-axis of the normal curve is called a z-value. Use the first table in the normal table for negative numbers. Look in the -1.0 row and the .00 column to find .1587. The answer is: 0.1587.
Example 2: What proportion of the observations are in this bin: (-∞, 2.00]?

Solution: Look the z-value 2.00 up in the second table for positive numbers, also in the normal table. Look in the 2.0 row and the 0.00 column to find .9772. The answer is 0.9772.
Example 3: What proportion of the observations are in this bin: (-3.00, 3.00]?

Solution: (-3.00, 2.00] can be written as the set-theoretic difference (-∞, 3.00] - (-∞, -3.00]. Look up these bins in the normal table: (-∞, 3.00] has the proportion 0.9987 and (-∞, -3.00] has the proportion 0.0013. Therefore the proportion of observations in (-3.00, 2.00] =
(-∞, 3.00] - (-∞, -3.00] is 0.9987 - 0.0013 = 0.9974.
Note: is does not matter whether we ask for the proportion of observations in (-3.00, 2.00], (-3.00, 2.00), [-3.00, 2.00), or [-3.00, 2.00]. They contain the same proportion of observations because the normal curve is an idealized continuous histogram where the the proportion of observations at a single point is always zero.
Example 4: What proportion of the observations are in this bin: (0.5, 1.5]?

Solution: (0.50, 1.50] = (-∞, 1.50] - (-∞, 0.50]. The the normal table gives the proportion of observations as 0.9332 - 0.6915 = 0.2417 = 24%.
If the normal histogram is not standard normal, any intervals must be first converted to z-scores.
Example 5: If the mean is 50 and the standard deviation is 10, convert 40 and 70 to z-scores. Solution:
and
Then the proportion of observations in the bin (-1, 2] = (-∞, 2] - (-∞, -1] is 0.9772 - 0.1587 = 0.8185.
Example 6: What is the 90th percentile for the standard normal curve.
Ans: The 90th percentile is the z-score such that the proportion of the observations in the bin (-&infty;, z] is 0.90. Find the area closest to 0.9000 in the normal table, which is 0.8977. This corresponds to the z-value 1.28.
Example 7: A population of giraffes has average height 16.5 feet with SD = 3.8 feet. What is the 25th percentile for giraffes?
Here are some practice problems on the area under the normal curve