To Documents

Areas under a Normal Histogram

Introduction

• A univariate dataset that has an approximately bell-shaped histogram is said to have a normal distribution.

• If x and SD+ really form a good description of a normal histogram, then given x and SD, we should be able to reconstruct the histogram; that is, we should be able to predict the proportion of observations in any bin of the form (-∞, a], (a, ∞], or [a, b].

Examples

1. We start with the simplest case of a normal histogram with center 0 and spread 1. Such a histogram is called a standard normal histogram.

   

2. Our tool for determining areas under the normal histogram is the standard normal table.

3. Example 1:   What proportion of the observations are in this bin: (-∞, -1.00]?

   

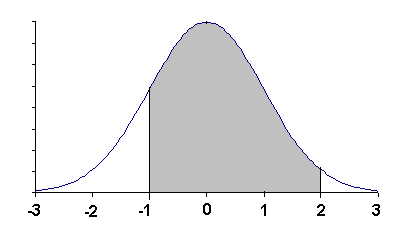
   Solution: The value -1.00 on the x-axis of the normal curve is called a z-value. Use the first table in the normal table for negative numbers. Look in the -1.0 row and the .00 column to find .1587. The answer is: 0.1587.

4. Example 2:   What proportion of the observations are in this bin: (-∞, 2.00]?

   

   Solution: Look the z-value 2.00 up in the second table for positive numbers, also in the normal table. Look in the 2.0 row and the 0.00 column to find .9772. The answer is 0.9772.

5. Example 3:   What proportion of the observations are in this bin: (-3.00, 3.00]?

   

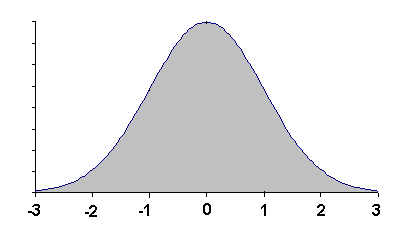
   Solution: (-3.00, 2.00] can be written as the set-theoretic difference (-∞, 3.00] - (-∞, -3.00]. Look up these bins in the normal table: (-∞, 3.00] has the proportion 0.9987 and (-∞, -3.00] has the proportion 0.0013. Therefore the proportion of observations in (-3.00, 2.00] =
   (-∞, 3.00] - (-∞,  -3.00] is 0.9987 - 0.0013 = 0.9974.

   Note: is does not matter whether we ask for the proportion of observations in (-3.00, 2.00], (-3.00, 2.00), [-3.00, 2.00), or [-3.00, 2.00]. They contain the same proportion of observations because the normal curve is an idealized continuous histogram where the the proportion of observations at a single point is always zero.

6. Example 4:   What proportion of the observations are in this bin: (0.5, 1.5]?

   

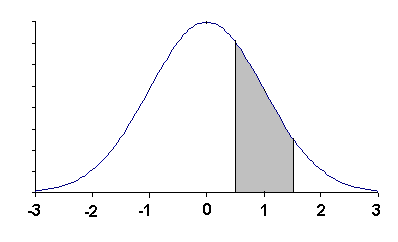
   Solution: (0.50, 1.50] = (-∞, 1.50] - (-∞, 0.50]. The the normal table gives the proportion of observations as 0.9332 - 0.6915 = 0.2417 = 24%.

7. If the normal histogram is not standard normal, any intervals must be first converted to z-scores.

8. Example 5: If the mean is 50 and the standard deviation is 10, convert 40 and 70 to z-scores. Solution:
   z = (x - x) / SD+ = (40 - 50) / 10 = -1

   and
   z = (x - x) / SD+ = (70 - 50) / 10 = 2

   Then the proportion of observations in the bin (-1, 2] = (-∞, 2] - (-∞, -1] is 0.9772 - 0.1587 = 0.8185.

   

9. Example 6: What is the 90th percentile for the standard normal curve. This means for what z-score is the area to the left of z equal to 0.90. Find the area closest to 0.9000 in the normal table, which happens to be 0.8977. This corresponds to the z-value 1.28.

10. Example 7: A population of giraffes has average height 16.5 feet with SD = 3.8 feet. What is the 25th percentile for giraffes?