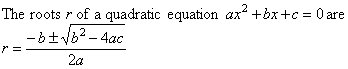415 lecture note #8 

[Ch 5] Recurrence Relations (2)

5.2 Solving Recurrence Relations

(1) Iteration Method (cont.)

• Now we know how to apply the iteration method to derive explicit formula (i.e., closed form) for recurrence relations of the form:
  • T(n) = T(n-c) + a
  • T(n) = T(n/c) + a

  where a is some number (constant or some expression which depends on n), and c is a constant.

• The next order of business is to prove the correctness of a formula (to verify that you didn't make any calculation mistake -- hopefully!!).

• Example1:   Tower of Hanoi

  Let T(n) be the number of moves required for n disks.  It can be defined in two ways, by recurrence relation and by closed formula, as:

  1. Recurrence relation

  T(n) = 2*T(n-1)+ 1, for all n >= 2, and
  T(1) = 1.

  2. Closed form

     T(n) = 2ⁿ - 1, for all n >= 1.

  So we need to prove that the two formulas are the same, for all n >= 1.

  --------------------------------------------------------------------------------
  Theorem:  Show if T(1), T(2),.., T(n) is the sequence defined by

  T(n) = 2*T(n-1) + 1, for all n >= 2, and T(1) = 1

  then, T(n) = 2ⁿ - 1, for all n >= 1.

  Proof:  by strong mathematical induction (with one base case).

  Basic Step (n = 1):

  • Recurrence:   T(1) = 1 ... by definition
  • Closed form:  T(1) = 2¹ - 1 = 1

  Therefore, the closed formula holds for n = 1. ........... (A)

  Inductive Step:

  Assume the closed formula holds for n-1, that is, T(n-1) = 2^n-1 - 1, for all n >= 2.
  Show the formula also holds for n, that is, T(n) = 2ⁿ - 1.

  T(n) = 2*T(n-1) + 1       ... by recursive definition 
         = 2*(2^n-1 - 1) + 1   ... by inductive hypothesis
         = 2*(2^n-1) - 2 + 1 
         = 2*(2^n-1) - 1 
         = 2ⁿ - 1 

  Therefore, the closed formula holds for n >= 2. ........... (B)

  By (A) and (B), the closed formula holds for all n >= 1.  QED.
  ---------------------------------------------------------------------

• Example 2:  Show if T(1), T(2),.., T(n) is the sequence defined by

  T(n) = -3*T(n-1)  for all n >= 1, and T(0) = 2

  then,  T(n) = 2*(-3)ⁿ

  Proof: 

          (will do in the class)

   

• The last order of business is to derive complexity.  We know how to do that already.

  Example:  T(n) = 2ⁿ - 1

  • T(n) = O(2ⁿ)  ... tightest one among all big-oh's for 2ⁿ
  • T(n) = W(2ⁿ)  ... tightest one among all omega's for 2ⁿ
  • T(n) = Q(2ⁿ)

(2) Characteristic Equation

• A recurrence relation that involves only the preceding term can be easily solved by iteration. Unfortunately, things tend to get a little messier if there is more than one preceding terms.  

  Example:  How can we derive a closed form for  f_n = f_n-1 + f_n-2 ?

• To solve those kind of patterns, we need more powerful tools.

Second order, Linear Homogeneous recurrence with Constant Coefficients

• Definition: A second order linear homogeneous recurrence with constant coefficients is a recurrence relation of the form

  a_n = c₁*a_n-1 + c₂*a_n-2  for all integers n >= some fixed integer,

  where c₁, c₂ are fixed real numbers with c₂ != 0.

• Notes on terminology:
  • second order -- expressions on the RHS contains the two previous terms (a_n-1 and a_n-2)
  • linear -- each term on the RHS is at the first power (i.e., (a_n-1)¹ and (a_n-1)¹)
  • homogeneous -- every term on the RHS involves a_i
  • constant coefficients -- c₁, c₂ are fixed constants, not involving n
• Examples:

  State whether each of the following is a second order linear homogeneous recurrence with constant coefficients. 

• Definition:  Given a recurrence relation a_n = A*a_n-1 + B*a_n-2, the characteristic equation of the relation is

  t² - At - B = 0

• Theorem: Consider a recurrence relation an = A*an-1 + B*an-2.  Let x and y be the roots of the characteristic equation for this relation.  Then there are any numbers C, D such that a) If x != y, then an = C*xn + D*yn       ... Distinct roots case b) If x = y, then an = C*xn + D*n*yn     ... Single root case Proof:  See Section 5.2.

   

• How can we use this theorem to derive closed forms???
• Example 1 (distinct roots):  Find the closed form for a recurrence relation

  a_n = a_n-1 + 2a_n-2,  for all integers n >= 2

  with initial conditions a₀ = 1 and a₁ = 8.

  Solution:

  The characteristic equation for this relation is t² - t - 2 = 0.  Computing the roots of this equation,

  t² - t - 2 = 0, so (t - 2)(t + 1) = 0

  we get  t₁ = 2 and  t₂ = -1.  Then from the theorem above, we know the closed form is written as:

  a_n = C*(2)ⁿ + D*(-1)ⁿ ........... (*)

  Now, we must solve for C and D (at this point, they are unknown).  To do so, we use the initial conditions -- by plugging in n = 0 (for a₀) and n = 1 (for a₁) in (*), and solve the two equations.

  a₀ = C*(2)⁰ + D*(-1)⁰ = C + D = 1   ..... (1)
  a₁ = C*(2)¹ + D*(-1)¹ = 2C - D = 8  ..... (2)

  To solve those equations, there are several ways.  Here is one way using substitution.
  We know C = 1 - D  by (1).  Substituting this in (2), we get

  2(1 - D) - D = 8
  2 - 2D - D = 8
  3D = -6
  D = -2,  so C = 1 + 2 = 3

  Then we have completely solved the closed form, which is now

  a_n = 3*(2)ⁿ + (-2)*(-1)ⁿ ........... (**)

  As the last note, the complexity of  this formula is Q(____).

• Example 2 (single root):  Find the closed form for a recurrence relation

  a_n = 4a_n-1 - 4a_n-2,  for all integers n >= 2

  with initial conditions a₀ = 1 and a₁ = 3.

  Solution:

  The characteristic equation for this relation is t² - 4t + 4 = 0.  Computing the roots of this equation,

  t² - 4t + 4 = 0, so (t - 2)² = 0

  we get  t = 2.  Then from the theorem above, we know the closed form is written as:

  a_n = C*(2)ⁿ + D*n*(2)ⁿ ........... (*)

  Now, we must solve for C and D (at this point, they are unknown).  To do so, we use the initial conditions -- by plugging in n = 0 (for a₀) and n = 1 (for a₁) in (*), and solve the two equations.

  a₀ = C*(2)⁰ + D*n*(2)⁰ = C  = 1   ..... (1)
  a₁ = C*(2)¹ + D*n*(2)¹ = 2C + 2D = 3  ..... (2)

  We know C = 1 by (1).  Substituting this in (2), we get

  2(1) + 2 D = 3
  2D = 1
  D = 1/2

  Then we have completely solved the closed form, which is now

  a_n = 1*(2)ⁿ + (1/2)*n*(2)ⁿ
       = (1 + (1/2)*n) * (2)ⁿ .................. (**)

  And the complexity of  this formula is Q(____).

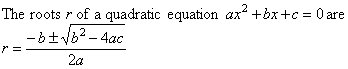• Algebra review

• More examples:  Find a closed form and theta complexity for each of the following recurrence relations.
  1. a_n = 4a_n-2, for all integers n >= 2, and a₀ = 1, a₁ = -1.
  2. a_n = 2a_n-1 + a_n-2, for all integers n >= 2, and a₀ = 1, a₁ = 4.
  3. a_n = 10a_n-1 - 25a_n-2, for all integers n >= 2, and a₀ = a₁ = 1.
  4. a_n = a_n-1 + a_n-2, for all integers n >= 2, and a₀ = 1, a₁ = 2.