415 Final Review WITH SOLUTIONS

csc 415 Review for Final
WITH SOLUTIONS

For the following algorithm segment, give T(n), the exact number of times the line x := x + 1 is executed. Assume n is any positive integer which is a power of 2.
```
j := n
while j >= 1 do
  begin
  for i := 1 to j do 
    x := x + 1
  j := j / 2
  end
```
ANSWER:

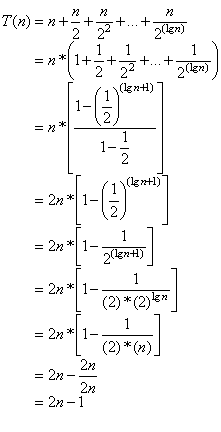
So, the closed form is T(n) = 2n - 1, for all n >= 1.
Prove the following statement formally.
Suppose f(x) = O(x^m) and g(x) = O(xⁿ), where m, n are positive integers. Then f(x)*g(x) = O(x^m+n).

ANSWER:

Proof: By defnition of big-Oh notation and the given assumptions on f and g, we know there exist c1, c2, x1, x2 such that

f(x) <= c1 * x^m (for all x >= x1) and g(x) <= c2 * xⁿ (for all x >= x2).

Since m, n are positive integers, we get

f(x) * g(x) < = c1 * c2 * x^(m+n), for all x >= max(x1, x2).

So, we can take c = c1 * c2, and n0 = max(x1, x2).
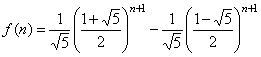
The closed form for fibonacci sequence is given/solved as follows.
1. Verify that this formula produces the same values as the recurrence relation for n = 1 and 2.
  ANSWER:
  - For n = 1:
    - Recurrence: f(1) = 1 ... by definition of fibonacci sequence
    - Closed form:
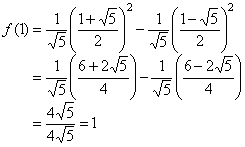
    So, f_recurrence (1) = f_closed (1).
  - For n = 2:
    - Recurrence: f(2) = 2 ... by definition of fibonacci sequence
    - Closed form:
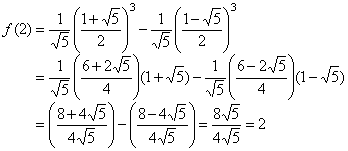
    So, f_recurrence (2) = f_closed (2).
2. Prove by strong mathematical induction that this formula is correct.
  ANSWER:
  
  Theorem: Fibonacci sequence defined recursively as
  
  f(n) = f(n-1) + f(n-2), f(1) = 1, f(2) = 2
  
  has an equivalent closed form
  
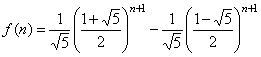
  Proof: by strong mathematical induction.
  
  Basic Step (n = 1, 2): As shown in part a. ... (A)
  
  Inductive Step: Assume the closed form holds for all f(i), 1 <= i < n. Show the closed form holds for f(n).
  
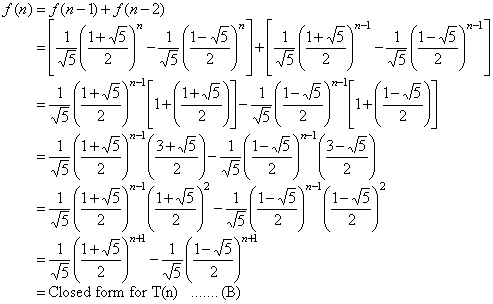
  From (A) and (B), the theorem is true.
A recursive algorithm find_min, which finds the minimum of a finite sequence of numbers, is given as follows (Section 3.4, Exercise #12).
Input: The sequence s1, s2, .., sn and the length n of the sequence.
Output: The minimum value in the sequence.
```
procedure find_min(s, n)
1. if n = 1 then
2.   return s1
3. else 
4.   begin
5.   x := find_min(s, n-1)
6.   if x < sn then
7.     return x
8.   else
9.     return sn
end find_min
```
Let T(n) be the number of times the comparison x < sn (line 6) is performed in the worst case.
1. Find a recurrence relation and an initial condition for T(n).
  ANSWER: T(n) = T(n-1) + 1, T(1) = 0
2. Solve the recurrence relation you answered in a. and derive a closed form.
  ANSWER: I skip the derivation here, assuming you know how to do this very well already. The closed form is
  
  T(n) = n - 1, for all n >= 1

csc 415 Review for Final WITH SOLUTIONS

csc 415 Review for Final
WITH SOLUTIONS