Updated 06/21/09

Text, p. 124

The Work-Energy Theorem is:  W_net = K_f - K_i = DKE, where W_net = F_netDx.

For conservative forces, the law of conservation of energy has the form: (KE_f - KE_i) + (PE_f - PE_i) = 0

where PE refers to any form of potential energy. In particular,
 
     GRAVITATIONAL POTENTIAL ENERGY is expressed as PE_grav = mgh, where h is the vertical distance of the center
     of mass from some arbitrarily chosen zero energy reference level.

     ELASTIC POTENTIAL ENERGY is expressed as PE_s = (1/2)kx², where x is the distance the spring is stretched or
     compressed and k is the elastic constant or stiffness constant, defined by Hooke’s law: F = -kx.

Gravitational and elastic forces are conservative forces; they depend only on position change.

For nonconservative forces, such as friction, a "work-like" quantity W_nc is defined to give a more general expression for energy conservation:

W_nc = (KE_f + PE_f) - (KE_i + PE_i) = DKE + DPE

To find W_nc for friction forces, use

W_nc = -fs,

where f is the magnitude of the friction force (f = µn) and s is the displacement of the body involved in the frictional interaction (e.g., a block slides a distance s while being slowed by friction). When a body is in motion and friction forces are involved, use the coefficient of kinetic friction, µ_k.

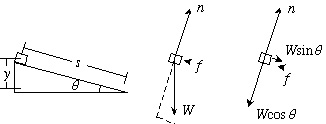
For "block on an incline" types of problems, a free body diagram illustrates the forces involved.

 
The friction force is:

f = µn = µWcosq = µmgcosq

If there is friction and the block starts from rest and PE = 0 at the bottom, conservation of energy gives us:

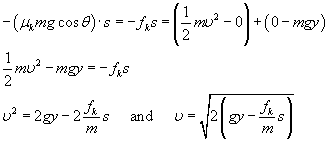
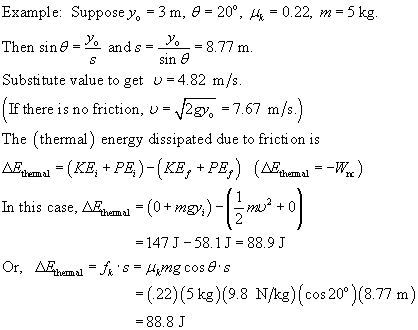
Now try this. A frictionless roller coaster has the dimensions shown here. The car has a velocity of magnitude u₁ at the top of a hill, u₂ at ground level, and dips to a point 4 m below ground level where its velocity has magnitude u₃.
  

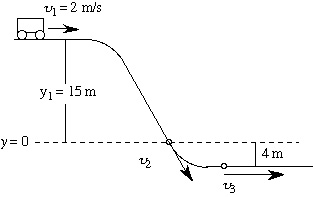
Use conservation of energy to find u₂ and u₃.

A spring-mass problem. A block of mass .005 kg is at rest on a spring that has been compressed a distance .04 m from its equilibrium position and locked in place. The spring lock is released and the block accelerates upward. The elastic constant of the spring is 75 N/m.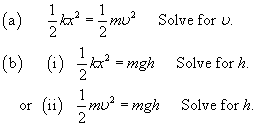
(a) Calculate the speed of the block when it loses contact with the spring.
(b) Calculate the maximum vertical position of the block.
Solutions
(a)    Apply conservation of energy. The elastic energy stored in the spring equals the kinetic energy acquired by the block,
(b)    Apply conservation of energy.
      (i)  The elastic energy stored in the spring equals the maximum gravitational potential energy of the system.
or  (ii)  The kinetic energy of the block when it loses contact with the spring equals the maximum gravitational potential energy of the system.

Roller coaster problem: u₂ = 17.3 m/s, u₃ = 19.4 m/s.

Spring-mass problem: (a) 4.9 m/s   (b) 1.22 m
 
Return