
1. Definitions

| A wrench is connected to a nut as shown in each
of these
pictures. In picture 1, a person pushes down and applies a force of 1 N
to the end of the wrench at a point 0.20 m from the center of the nut.
In picture 2, an object with a weight of 1 N is hung from the end of
the
wrench at a point 0.20 m from the center of the nut. In picture 3, the
same object is hung from the same point, but from a shorter string. In
picture 4, the same 1 N force is applied at the same point, but at an
angle
of 135o up from the horizontal. In each case the wrench will
tend to rotate, and if it does the nut will turn. As you can see, the
direction
of rotation (clockwise or counterclockwise) will depend on the
direction
in which the force is applied.
Compare pictures 1, 2 and 3. Will the initial turning effect be the same in each case? The measure of the "turning effect" or rotational tendency is called torque. |
 |
| Torque can be defined in terms of these quantities: force of magnitude F, the distance r from the point of application of the force to the fulcrum, direction angle q between the lever arm and the line of action of the force. : t = rFsinq The sine function appears
because
only the component of the force perpendicular to the lever arm will
tend
to produce rotation. In the case shown here, the rotation direction is
counterclockwise. By definition, the torque in this case is positive.
t = Frsinq. Scroll up and look at pictures 1, 2 and 3. The forces all have the same magnitude and the same line of action, so they all produce the same torque. In these cases: t = Frsinq = (.2 m)(1 N)(sin90o) = 0.2 mN The sign is positive because the rotational tendency is counterclockwise. |
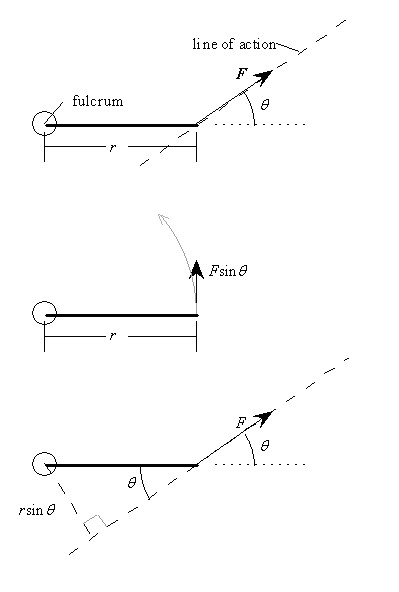 |
Note that torque seems to have the same units as work and energy. But torque is not work or energy! It is not correct to say that 1 mN of torque equals 1 joule of torque. It is a good idea to distinguish torque from work and energy by using the "meter-newton" (mN) as the unit of torque and the "newton-meter" (or joule) as the unit of work and energy. What are the sign and the magnitude of the torque produced by the force applied to the wrench in picture 4 above? (Check your answer.)
2. Rotational Equilibrium
| Recall that the lines of action of concurrent forces
intersect
at a point. In this case the conditions for equilibrium (in two
dimensions)
are:
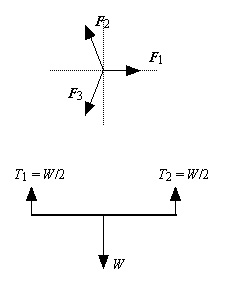
SFx = 0, SFy = 0. Consider a situation in which the lines of action of the forces are parallel (nonconcurrent): A uniform bar of weight W is supported by two vertical cords connected to the ends of the bar. You have seen that in this case the tensions in the cords are equal to half the weight of the bar. There is now an added condition for equilibrium. The sum of the torques must equal zero. All the torques must be calculated with reference to the same point designated as the fulcrum, and any point may be chosen as the fulcrum. A helpful problem-solving strategy is to choose a fulcrum which eliminates as many unknown quantities as possible. With reference to the force diagram shown here, to find the tensions in the cords, designate the left or right end of the bar as the fulcrum. We will choose the left end and call the length of the bar L. If the bar is uniform, the weight of the bar can be located at the middle, a distance L/2 from the fulcrum. Now write the two conditions for equilibrium. (Only two conditions apply because in this problem there are no horizontal forces.) SFy = 0 = T1 + T2 - W St = 0 = (L)(T2) - (L/2)(W) The solution of the torque equation is, of course, T2 = W/2. Substitution in the force equation yields T1 = W/2, as expected. |
 |
| When the forces are nonconcurrent, but not all are vertical,
all three
conditions for equilibrium must be used. Here is an example. A
sign
of weight W = 30 N is hung 1.5 m from the left end of a uniform
bar of weight Wb = 40 N and length 2 m. The left end
of the bar is anchored to a wall and the right end is connected to the
wall by a cable that makes an angle of 30o with the
horizontal.
Find the tension in the cable and the support forces applied to the bar
by the cable.
Solution. Carefully draw the free body diagram of the bar; label and identify all the forces applied to the bar. Here, as you can see, there are five forces, the weights of the bar and the sign, the tension in the cable, and the horizontal and vertical wall support forces. There must be a horizontal force H in the direction shown because the only other horizontal force is the x component of the tension in the cable, and this points to the left. Note that in the free body diagram lines have been draw through the tension vector to indicate that it has been replaced by its components, where, of course, the magnitudes of these components are: |
 |
Tx = Tcos 30o and Ty = Tsin 30o.
Write the conditions for equilibrium:
SFx
= H -Tx
= 0 = H -Tcos
30o.
SFy
= V + Ty -Wb-W
= V + Tsin30o -Wb-W
= 0
St =
(2 m)(Ty) -
(1 m)(Wb) -
(1.5 m)(W) = 0
By choosing the left end of the bar as the fulcrum we have eliminated all but one unknown force from the torque equation. This equation can be solved for T and the two force equations can then be solved for H and V. Do this and check your answers.
|
t = Frsinq
= -(.2
m)(1 N)(sin135o)
|
 |
Answer to "Try this": The second cord should be placed a distance 3L/4 from the left end of the bar.
T =85 N, H = 73.6 N, V = 42.5 N