(In this tutorial, as in the text, chapter 6, "momentun" means "linear momentum." It is assumed that there are no rotations.)
We confine ourselves to interactions that are one-dimensional and are either (i) totally elastic or (ii) totally inelastic. The vector properties of both velocity and momentum can be described by the use of positive and negative signs. Masses and velocities must always be identified by subscripts (e.g., m1, u2i) or the use of upper and lower case letters (e.g., m and M refer to two different mass values). The use of subscripts is preferred.
Definitions:

Impulse and Momentum.

Conserved quantities
1. In all closed system (no forces applied from outside the system) total system momentum remains constant before, during and after the interaction.
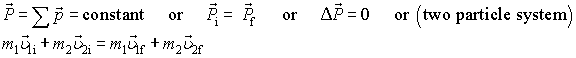
A corollary of this is that the center of mass velocity of the system is also constant.
2. In a one-dimensional totally elastic interaction, the conserved quantities are:
(i) Total system momentum. m1u1i +m2u2i = m1u1f +m2u2f
(ii) Total system kinetic energy.
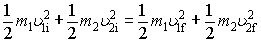
(Note that all the kinetic energy terms are positive.)
(iii) The magnitude of the relative velocity. See text equation (7-14):
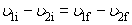
Combining the relationships in (i) and (ii) yields the following working equations for totally elastic collisions.
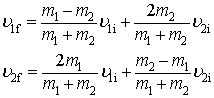
3. In a one-dimensional totally inelastic interaction, total system momentum is conserved.
The interacting particles have a common velocity after the interaction has occurred.
m1u1i
+m2u2i
= (m1+m2)u2f
4. In an "explosion" the particles have a common velocity before the interaction.
(m1+m2)ui = m1u1f
+m2u2f