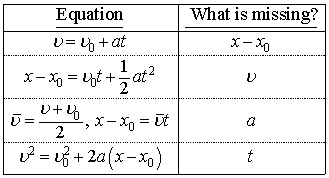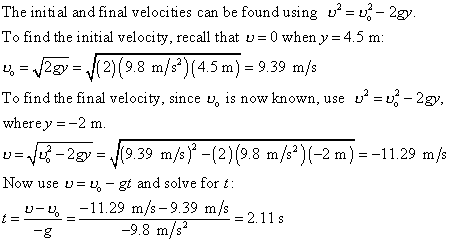"Uniform" means "constant." If a is constant and not zero, then   x = u^.t  does not apply!

Quantities of Interest

Time (t) - Clock reading. t and Dt are always positive.

Position (x or y or z) - An object's location with reference to the origin of a coordinate system.

Displacement  - Change in position. For one-dimensional motion along the x-axis, displacement is: Dx = x- x_o.
                          The expression "distance moved" is more or less synonymous with displacement.
                          You will need to look at the wording and the context of the problem.

Velocity (u) - The instantaneous velocity at any time t is the slope of the x vs. t graph at that point in time.
                       Our text uses u_o to indicate initial velocity and u to indicate final velocity.

Acceleration (a) - The instantaneous acceleration at any time t is the slope of the u vs. t graph at that point in time.

The magnitude of a quantity is its absolute value, always a positive number.

Test yourself (1). What is the algebraic sign of the velocity of an object under these conditions?
(a) On the positive x-axis and moving toward the origin.
(b) On the negative x-axis and moving away from the origin.
(c) On the negative x-axis and moving toward the origin.
(d) On the positive x-axis and moving away from the origin.
Check your answers.

Positive acceleration means
     either u is in the  + x direction and is increasing in magnitude,
     or u is in the  -x direction and is decreasing in magnitude.
Negative acceleration means
     either u is in the  + x direction and is decreasing in magnitude,
     or u is in the  -x direction and is increasing in magnitude.

Test yourself (2). For each of these cases, what is the sign of the acceleration?
(a) u_o = -2 m/s, u = -1 m/s.
(b) u_o = +3 m/s, u = 0 m/s.
(c) u_o = -2 m/s, u = -4 m/s.
(d) u_o = +2 m/s, u = +6 m/s.
Check your answers.

Basic Relationships
 

A Good Problem-Solving Strategy Identify the known variables and the missing quantities. Select the equation or equations that will enable you to find the missing quantities. Sketching a velocity vs. time graph is usually helpful. Work through the algebra of the solution. Put in numbers and calculate as close to the end of the  solution as possible. Check units.

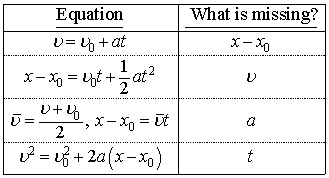
Sample Problem Solutions

 1. A truck moving at 12.0 m/s brakes uniformly to a stop in 8.30 seconds. Calculate the distance that the truck travels while braking.

Given: u_o = 12 m/s, u = 0, t = 8.3 s.  Missing: a, x.  Find: x.

Sketch a graph of u vs. t.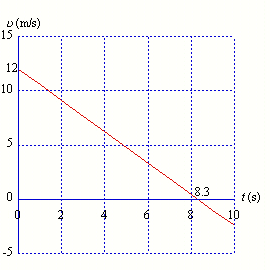 

2.  A ball is thrown into the air and rises to a maximum height of 4.5 m. How much time does it take for the ball to return to a point 2 m below its starting point?

Given: y_max = 4.5 m, y_final = -2 m, a = -9.8 m/m/s².  Missing: u_o, u_final, t.

Sketch a u vs. t graph of the motion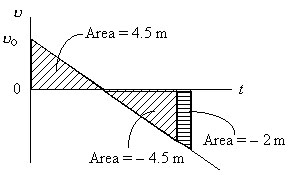  

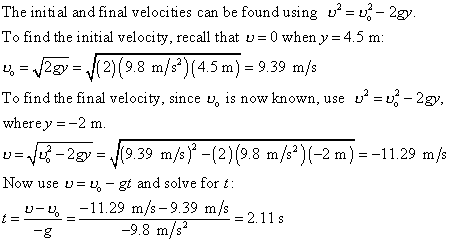
Test yourself (1) Answers: (a) and (b) negative, (c) and (d) positive.

Test yourself (2) Answers: (a) positive, (b) and (c0 negative, (d) positive.

Back to top

Return