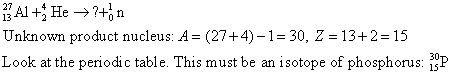1. Terminology and Symbolism

      Text (p. 967): "Rest energy" is E_o = mc². If m is in kg, E_o is in joules.

       Unified mass unit: 1 u = 1.660540 x 10^-27 kg = 931.6 MeV/c²

       Nutron and electron masses are in the table of Physical Constants, inside text fron cover..
       Atomic masses (neutral atoms) are in Appendix B, pages 1119-1120
       The mass values in this table include the extranuclear electrons.

1. Binding Energy

The general principle for calculating the binding energy of a nucleus is based on conservation of energy:

(mass difference) = (total mass of component parts) - (mass of nucleus)
or
Dm = [Zm_p + (A-Z)m_n] - m_N

where m_p is the proton mass, m_n is the neutron mass and m_N is the mass of the nucleus.
(The value to be used for m_p is that of the neutral hydrogen atom; this takes the electron masses into account.)

If the masses are in unified mass units (u), then the binding energy is

E_b = (Dm)(931.5 MeV/u)

Example. Calculate the binding energy of ²⁰₁₀Ne.

Z = 10 and A = 20, N = 10. The masses are: m_p = 1.007825 u, m_n = 1.008665 u, m_N = 19.992435 u.

Dm = [(10)(1.007825 u) + (10)(1.008665 u)] - 19.992435 u = .1772465 u

E_b = (.172465 u)(931.5 MeV/u) = 161 MeV

The "binding energy per nucleon" is (161 Mev)/(20 nucleons) = 8.03 MeV/nucleon

2. Radioactive Decay

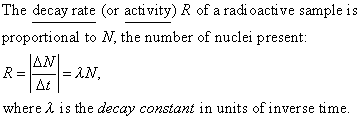
If there are N_o nuclei present at time t = 0, then the number N present at a later time t is given by:

N = N_oe^-lt

If the decay rate is R_o at time t = 0, then the decay rate R at a later time t is given by:

R = R_oe^-lt

The usual units for R are the curie (Ci), 3.7 x 10¹⁰ decays/s and the becquerel (Bq), 1 decay/s.
 

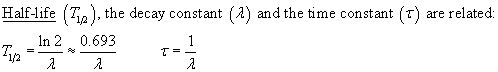
Example

A radioactive sample has a half-life of 140 days. Calculate the time required for the activity to be one-tenth of its initial value.

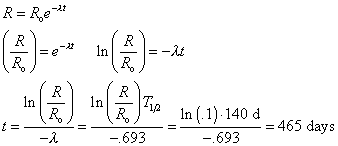
3. Radiactive Decay Schemes

Conservation of nucleon number and conservation of charge must be satisfied.

(a) Alpha Decay

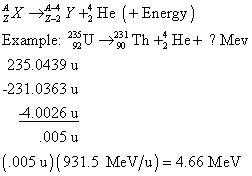
In this example, A = (A - 4) + 4 and Z = (Z - 2) + 2. Nuncleon number and charge are conserved.

(b) Beta Decay (positive and negative)

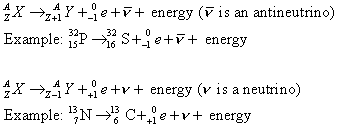
(c) Gamma Decay

A nucleus with excess energy (in an "excited state") emits the excess energy in the form of a gamma photon.

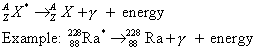
(d) Nuclear Reactions

Nucleon number, charge number, and mass-energy must all be conserved.

Example. An energetic alpha particle penetrates a beryllium nucleus, forms an unstable carbon-13 nucleus,
which then disintegrates. The "Q" of the reaction is the energy difference between the total mass of the
particles present before and after the reaction.

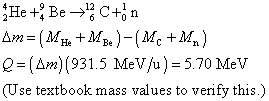
Example. Supply the missing product nucleus.

Return