BTrees

B-trees: Perfectly Height-balanced M-way search trees

A B-tree is an M-way search tree with two special properties:

It is perfectly balanced: every leaf node is at the same depth.

Every node, except perhaps the root, is at least half-full, i.e. contains M/2 or more values (of course, it cannot contain more than M-1 values). The root may have any number of values (1 to M-1).

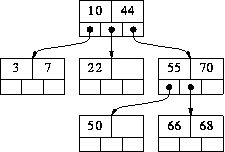
The 3-way search tree above is clearly not a B-tree. Here is a 3-way B-tree containing the same values:

And here is a 5-way B-tree (each node other than the root must contain between 2 and 4 values):

In the descriptions of our algorithms, we assume that M is odd; therefore each node (other than the root) must contains between (M-1)/2 and M-1 values.

Insertion into A B-Tree

To insert value X into a B-tree, there are 3 steps:

using the SEARCH procedure for M-way trees (described above) find the leaf node to which X should be added.

add X to this node in the appropriate place among the values already there. Being a leaf node there are no subtrees to worry about.

if there are M-1 or fewer values in the node after adding X, then we are finished.
If there are M nodes after adding X, we say the node has overflowed. To repair this, we split the node into three parts:

Left:
the first (M-1)/2 values
Middle:
the middle value (position 1+((M-1)/2)
Right:
the last (M-1)/2 values

Notice that Left and Right have just enough values to be made into individual nodes. That's what we do... they become the left and right children of Middle, which we add in the appropriate place in this node's parent.
But what if there is no room in the parent? If it overflows we do the same thing again: split it into Left-Middle-Right, make Left and Right into new nodes and add Middle (with Left and Right as its children) to the node above. We continue doing this until no overflow occurs, or until the root itself overflows. If the root overflows, we split it, as usual, and create a new root node with Middle as its only value and Left and Right as its children (as usual).

Example of Inserting Values to B-tree

For example, let's do a sequence of insertions into this B-tree (M=5, so each node other than the root must contain between 2 and 4 values):
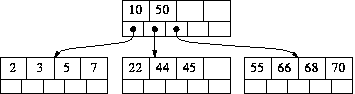
Insert 17: Add it to the middle leaf. No overflow, so we're done.

Insert 6: Add it to the leftmost leaf. That overflows, so we split it:

Left = [ 2 3 ]
Middle = 5
Right = [ 6 7 ]
Left and Right become nodes; Middle is added to the node above with Left and Right as its children. The node above (the root in this small example) does not overflow, so we are done.
Insert 21: Add it to the middle leaf. That overflows, so we split it:

left = [ 17 21 ]
Middle = 22
Right = [ 44 45 ]
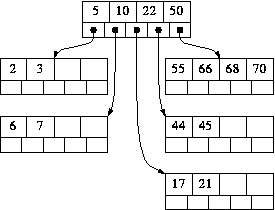
Left and Right become nodes; Middle is added to the node above with Left and Right as its children.
The node above (the root in this small example) does not overflow, so we are done.
Insert 67: Add it to the rightmost leaf. That overflows, so we split it:

Left = [ 55 66 ]
Middle = 67
Right = [ 68 70 ]
Left and Right become nodes; Middle is added to the node above with Left and Right as its children. But now the node above does overflow. So it is split in exactly the same manner:

Left = [ 5 10 ] (along with their children)
Middle = 22
Right = [ 50 67 ] (along with their children)

Left and Right become nodes, the children of Middle. If this were not the root, Middle would be added to the node above and the process repeated. If there is no node above, as in this example, a new root is created with Middle as its only value.

The tree-insertion algorithms we're previously seen add new nodes at the bottom of the tree, and then have to worry about whether doing so creates an imbalance. The B-tree insertion algorithm is just the opposite: it adds new nodes at the top of the tree (a new node is allocated only when the root splits).

B-trees grow at the root, not at the leaves. Because of this, there is never any doubt that the tree is always perfectly height balanced: when a new node is added, all existing nodes become one level deeper in the tree.

Deleting A Value from A B-tree

Recall our deletion algorithm for binary search trees: if the value to be deleted is in a node having two subtrees, we would replace the value with the largest value in its left subtree and then delete the node in the left subtree that had contained the largest value (we are guaranteed that this node will be easy to delete).

We will use a similar strategy to delete a value from a B-tree. If the value to be deleted does not occur in a leaf, we replace it with the largest value in its left subtree and then proceed to delete that value from the node that originally contained it.

For example, if we wished to delete 67 from the above tree, we would find the largest value in 67's left subtree, 66, replace 67 with 66, and then delete the occurrence of 66 in the left subtree. In a B-tree, the largest value in any value's left subtree is guaranteed to be in leaf.

Therefore wherever the value to be deleted initially resides, the following deletion algorithm always begins at a leaf.

To delete value X from a B-tree, starting at a leaf node, there are 2 steps:

Remove X from the current node. Being a leaf node there are no subtrees to worry about.

Removing X might cause the node containing it to have too few values.
Recall that we require the root to have at least 1 value in it and all other nodes to have at least (M-1)/2 values in them. If the node has too few values, we say it has underflowed.
If underflow does not occur, then we are finished the deletion process. If it does occur, it must be fixed. The process for fixing a root is slightly different than the process for fixing the other nodes, and will be discussed afterwards.

Example of Deleting Values from A B-tree

How do we fix a non-root node that has underflowed? Let us take as a specific example, deleting 6 from this B-tree (of degree 5):
Removing 6 causes the node it is in to underflow, as it now contains just 1 value (7). Our strategy for fixing this is to try to `borrow' values from a neighbouring node. We join together the current node and its more populous neighbour to form a `combined node' - and we must also include in the combined node the value in the parent node that is in between these two nodes.
In this example, we join node [7] with its more populous neighbour [17 22 44 45] and put `10' in between them, to create
[6 7 10 17 22 44 45]
How many values might there be in this combined node?

The parent node contributes 1 value.
The node that underflowed contributes exactly (M-1)/2-1 values.
The neighbouring node contributes somewhere between (M-1)/2 and (M-1) values.
The treatment of the combined node is different depending on whether the neighbouring contributes exactly (M-1)/2 values or more than this number.
Case 1: Suppose that the neighbouring node contains more than (M-1)/2 values. In this case, the total number of values in the combined node is strictly greater than 1 + ((M-1)/2 - 1) + ((M-1)/2), i.e. it is strictly greater than (M-1). So it must contain M values or more.
We split the combined node into three pieces: Left, Middle, and Right, where Middle is a single value in the very middle of the combined node. Because the combined node has M values or more, Left and Right are guaranteed to have (M-1)/2 values each, and therefore are legitimate nodes. We replace the value we borrowed from the parent with Middle and we use Left and Right as its two children. In this case the parent's size does not change, so we are completely finished.
This is what happens in our example of deleting 6 from the tree above. The combined node [6 7 10 17 22 44 45] contains more than 3 values, so we split it into:

Left = [ 6 7 10 ]
Middle = 17
Right = [ 22 44 45 ]
Then put Middle into the parent node (in the position where the `10' had been) with Left and Right as its children:
Case 2: Suppose, on the other hand, that the neighbouring node contains exactly (M-1)/2 values. Then the total number of values in the combined node is 1 + ((M-1)/2 - 1) + ((M-1)/2) = (M-1)
In this case the combined node contains the right number of values to be treated as a node. So we make it into a node and remove from the parent node the value that has been incorporated into the new, combined node. As a concrete example of this case, suppose that, in the above tree, we had deleted 3 instead of 6. The node [2 3] underflows when 3 is removed. It would be combined with its more populous neighbour [6 7] and the intervening value from the parent (5) to create the combined node [2 5 6 7]. This contains 4 values, so it can be used without further processing. The result would be:

It is very important to note that the parent node now has one fewer value. This might cause it to underflow - imagine that 5 had been the only value in the parent node. If the parent node underflows, it would be treated in exactly the same way - combined with its more populous neighbour etc. The underflow processing repeats at successive levels until no underflow occurs or until the root underflows (the processing for root-underflow is described next).
Now let us consider the root. For the root to underflow, it must have originally contained just one value, which now has been removed. If the root was also a leaf, then there is no problem: in this case the tree has become completely empty.
If the root is not a leaf, it must originally have had two subtrees (because it originally contained one value). How could it possibly underflow?
The deletion process always starts at a leaf and therefore the only way the root could have its value removed is through the Case 2 processing just described: the root's two children have been combined, along with the root's only value to form a single node. But if the root's two children are now a single node, then that node can be used as the new root, and the current root (which has underflowed) can simply be deleted.
To illustrate this, suppose we delete 7 from this B-tree (M=5):

The node [3 7] would underflow, and the combined node [3 10 18 20] would be created. This has 4 values, which is acceptable when M=5. So it would be kept as a node, and `10' would be removed from the parent node - the root. This is the only circumstance in which underflow can occur in a root that is not a leaf. The situation is this:
Clearly, the current root node, now empty, can be deleted and its child used as the new root.