Graphs

1. Basic definitions

• Graph G = (V, E) where V is a set of vertices and E is a set of edges. Each edge e Î E is a 2-tuple of the form (v, w) where v, w Î V, and e is called an incident on v and w.

  
  

• An edge may be directed or undirected.
• An edge may also have a weight.

  
  

• A path is a sequence of vertices connected by edges, and represented as a sequence in 2 ways:
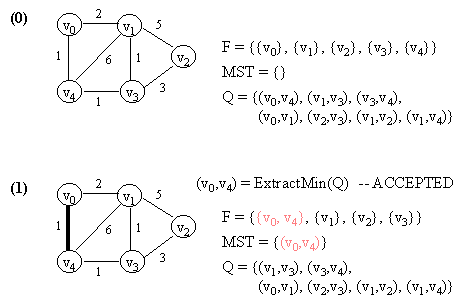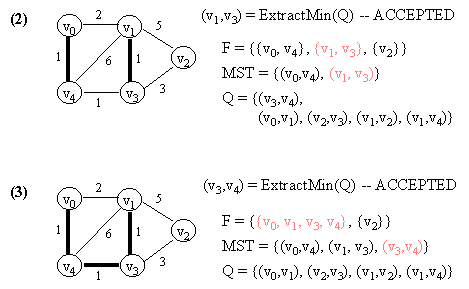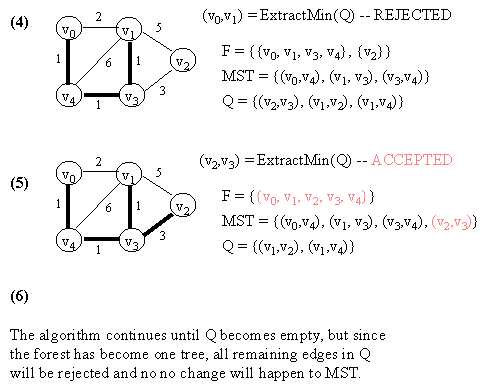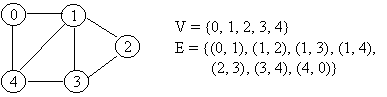
  • (v₀, e₁, v₁, e₂, v₂,..,v_n-1, e_n, v_n) -- alternating vertices and edges
  • (v₀, v₁, v₂,..,v_n-1, v_n) -- vertices only
• A graph is connected if, for any vertices v and w, there is a path from v to w.

  

2. Representing Graphs

• Adjacency matrix
  • n by n matrix, where n is number of vertices
  • A(m,n) = 1 iff (m,n) is an edge, or 0 otherwise
  • For weighted graph: A(m,n) = w (weight of edge), or positive infinity otherwise

    

• Adjacency list
  • Each vertex has a linked list of edges
  • Edge stores destination and label
  • Better when adjacency matrix is sparse

    

3. Graph Traversal

• Walk through a graph systematically in a predefined order -- Depth-first, or Breadth-first. 

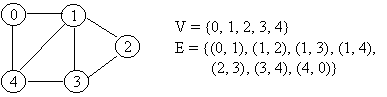
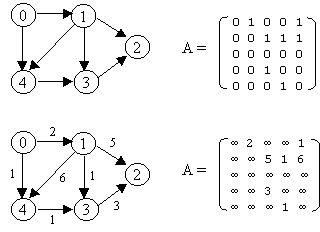
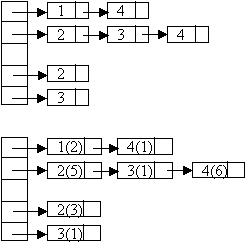
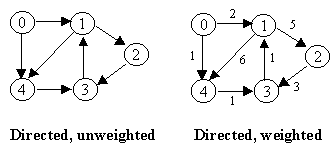
3.1 Depth-First Traversal

• Follow a path until it ends, or until a cycle.  Use a stack.

  

• Algorithm:

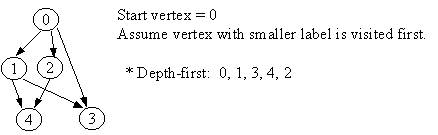
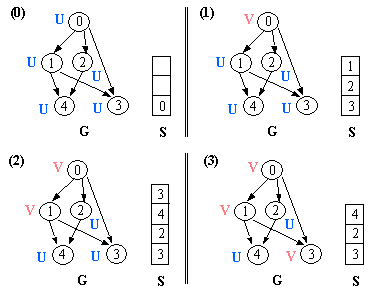
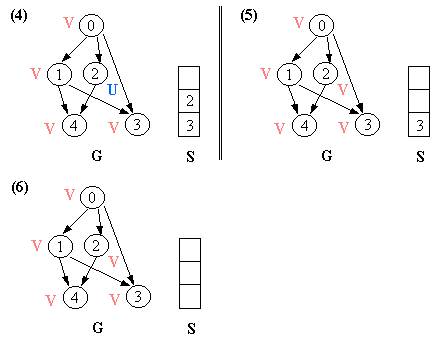
  Let G = (V, E) is a graph which is represented by an adjacency matrix Adj.  Assume that nodes in a graph record visited/unvisited information. 

  procedure DEPTH-FIRST (G)
  1. Initialize all vertices as "unvisited".
  2. Let S be a stack.
  3. Push the root on S.
  4. While S not empty, do
  5.   begin
  6.   Let n <- Pop S.
  7    If n is marked as "unvisited", then
  8.     begin
  9.     Mark n as "visited", and output n to the terminal.
  10.     For each vertex v in Adj[n], do
  11.       If v is marked as "unvisited", then // this test is actually redundant
  12.         push v on S.
  13.    end
  14.  end

  
  
  

3.2 Breadth-First Traversal

• Visit nodes layer-by-layer.  Use a queue.

  

• Algorithm :

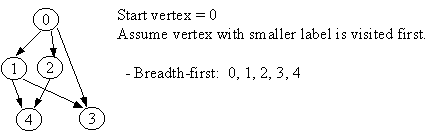
  procedure BREADTH-FIRST (G)
  1. Initialize all vertices as "unvisited".
  2. Let Q be a queue.
  3. Enqueue the root on Q.
  4. While Q not empty, do
  5.   begin
  6.   n <- Dequeue Q.
  7.   If n is marked as "unvisited", then
  8.     begin
  9.     Mark n as "visited", and output n to the terminal.
  10.     For each vertex v in Adj[n], do
  11.       If v is marked "unvisited", then
  12.         enqueue v on Q.
  
  
  13.    end
  14.  end
  

4. Graph Search

• Two search methods corresponding to the two traversal schemes above: Depth-First Search (DFS) and Breadth-First Search (BFS).
• Terminate search/traversal as soon as the item is found.

5. Minimum Spanning Trees (MST) 

• A minimum spanning tree T of an undirected graph G is a subgraph of G that connects all the vertices in G at the lowest total cost.

  

• MST is used as one of the most important tools to analyze computer networks (e.g. cabling, network load capacity, optimal flow).
• Two algorithms: Prim's algorithm and Kruskal's algorithm.
• They are both greedy algorithms.

6.1 Prim's Algorithm

• Maintains ONE TREE throughout the algorithm, and make it grow by adding edge by edge.
• The idea is to select the next edge 
  • which is adjacent from any vertex/node in the tree built so far; and
  • which has the lowest weight among alternatives (i.e., all edges connected from any vertex/node in the tree built so far).

  

• Algorithm:

  Let G = (V, E) which is represented by an adjacency list Adj. Some support data structures:

  • d is an array of size |V|.  Each d[i] contains the shortest distance for vertex i
  • Q is a priority queue of UNKNOWN vertices.
  • p is an array of size |V|.  Each P[i] contains the parent of vertex i.
  • s is the source vertex.

  PRIM(G, s)
  1. Initialize d[s] with 0, P[s] with 0, and
      all other d[i] (i!=s) with a positive infinity and
                p[i] (i!=s) with 0.
  2. Q <- V  // initialize Q with all vertices as UNKNOWN
  3. while Q not empty do
  4.   begin
  5.   u <- ExtractMin(Q)  // Q is modified
  6.   Mark u as KNOWN     // Dequeing u is the same as marking it as KNOWN
  7.   for each vertex v in Adj[u] do
  8.     begin
  9.     if v is UNKNOWN and d[v] > weight(u, v), then do
  10.      begin
  11.      d[v] = weight(u, v)  // update with shorter weight
  12.      p[v] = u             // update v's parent as v
  13.      end
  14.    end
  15.  end
  

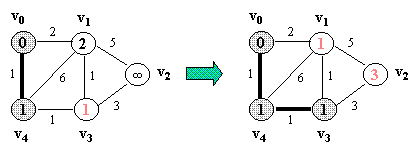
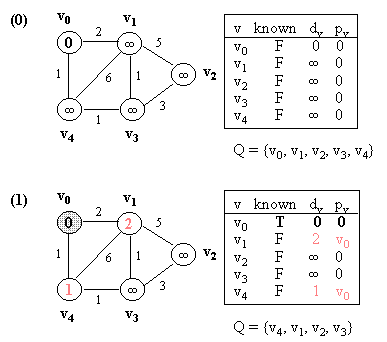
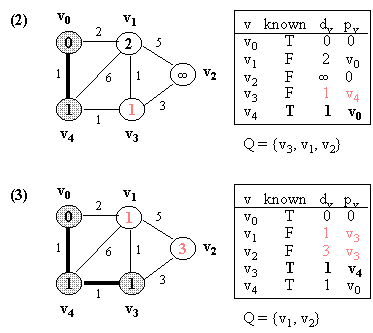
• Example (NOTE: v0 is the source vertex, and d[i] for each vertex i is also indicated in its circle):

  
  
  

6.2 Kruskal's Algorithm

• The main idea is to
  • start with a set (called forest) of singleton trees, and
  • merge two trees at a time, unless it creates a cycle in the merged tree, until the forest becomes one tree.
• The algorithm makes use of notions such as forest and union-find algorithm.  But even without knowing them, you can intuitively understand Kruskal's algorithm quite easily.
• Algorithm:

  Let G = (V, E) which is represented by an adjacency list Adj. Some support data structures:

  • F is the forest -- a set of all (partial) trees.
  • MST is the minimum spanning tree, represented by a set of edges.
  • Q is a priority queue of edges.

  KRUSKAL(G)
  1. Let F be a set of singleton set of all vertices in G.
  2. MST <- {}
  3. Q <- E
  4. while Q not empty do
  5.   (u, v) <- ExtractMin(Q)            // Q is modified
  6.   if FIND-SET(u) != FIND-SET(v) then // FIND-SET(i) returns the set in F
                                          // which vertex i belongs to.
                                          // This effectively does cycle check.
                                          // If ACCEPTED,
  7.     begin
  8.     merge(FIND-SET(u),FIND-SET(v)) in F
  9.     MST <- MST Union {(u, v)}
  10.    end
  11. return MST.

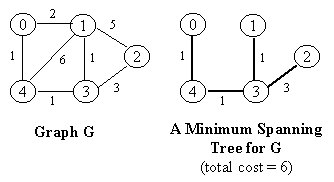
  NOTE: In the figure below, a number in a vertex indicates the vertex number (NOT any kind of value).