[W: 4.1-4.2, 4.6] Trees, Binary Trees

1. Basic Concepts

• Tree is a nonlinear/nonsequential data structure where nodes are organized in a hierarchical way.

  

• Some terminologies
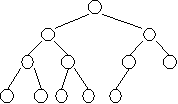
  • path from node n1 to nk -- a sequence of nodes [n1, n2,.., nk]
  • length of a path -- number of edges in the path
  • depth (level) of a node -- length of the path from the root to the node
  • height of a node -- length of the path from the node to the deepest node in the subtree rooted by that node
  • height of a tree -- height of the root
• Definitions for nodes in a tree
  • leaf node -- a node with no children
  • internal node -- any node in a tree that is not a leaf

2. Binary Trees

• Binary tree is a special kind of a tree in which nodes have at most 2 children (none or left-child only or right-child or both).

• When a tree of height d has all nodes filled from level 0 to d-1, and the leaf nodes at the d^th level are filled from the left-most position, then the tree is called a complete binary tree. 

  

• If every node in a binary tree has either 2 children or 0, then the tree is called a full binary tree.

  
  

3. Mathematical Properties of binary trees

1. Number of nodes on each level i is at most 2ⁱ
   • level 0: 2⁰ = 1 ... root
   • level 1: 2¹ = 2
   • level 2: 2² = 4

   Those are upper bound numbers which hold when a tree is fully expanded (i.e., a tree of depth d is complete and all nodes at depth 0 through d-1 have two children).

2. Total number of nodes in a (general) binary tree of depth d is
   • upper bound: 2⁰ + 2¹ + 2² + .. + 2^d = 2^d+1 -1 (by geometric sequence) -- when a tree is fully expanded
   • lower bound: d + 1 -- when all internal nodes have 1 child (called a degenerate tree)

3. Depth of a binary tree with N nodes >= floor(lgN)
   • lower bound: floor(lgN) .. when a tree is fully expanded
   • upper bounf: N - 1 .. , when a tree is a degenerate tree

     e.g. floor(lg31) = 4

Exercises:

1. How many nodes are in a fully expanded binary tree of depth 5? Of them, how many are internal, and how many are leaf nodes?

   
   
   

2. What is the depth of a complete binary tree with 200 nodes?
   
   
   
   

4. Class BinaryNode

class BinaryNode
{
  // constructors
  BinaryNode( Comparable o ) { element = o; }
  BinaryNode( Comparable o, BinaryNode lt, BinaryNode rt )
  {
    element  = o;
    left     = lt;
    right    = rt;
  }

  // fields
  Comparable element;
  BinaryNode left;
  BinaryNode right;
}

• e.g. Building a tree (resulting picture below)

  

   BinaryNode root;  // start from an empty tree
  
  
  
  
  
  
  
  

• e.g. Adding a node -- Add 'Z' as the right child of 'Y', when temp is pointing at 'Y'

  

  
  
  
  
  
  

5. Inorder/Preorder/Postorder Tree Traversals

• Given the following tree

             A
           /   \
          B     F
           \   / 
           C   G
          / \
         D   E

There are three different orders to visit nodes:

1. Preorder -- 1) visit current node, 2) go left, then 3) go right
2. Inorder -- 1) go left, 2) visit current node, then 3) go right
3. Postorder -- 1) go left, 2) go right, then 3) visit current node

Preorder:  A B C D E F G
Inorder:   B D C E A G F
Postorder: D E C B G F A

• Using recursion, functions for those traversal strategies can be easily written.

  void inorder(BinaryNode node)
  {
    if (node != null)
    {
      inorder(node.left);               // go left first -- recursive call
      System.out.println(node.element); // then visit (print the node data)
      inorder(node.right);              // and then go right -- recursive call
    }
  }

• Other two, preorder and postorder are straight-forward.

6. Recursion and Binary Trees

• Size of a tree (returns the total number of nodes in a (sub)tree)

  int SizeOfTree(BinaryNode n)
  {
    if (n == null)
      return 0;
    else
      return (1 + SizeOfTree(n.left) + SizeOfTree(n.right));
  }

• Height of a tree (returns the length of path to the deepest node)

  int TreeHeight(BinaryNode n)
  {
    if (n == null)
      return -1;
    else
      return (1 + Max(TreeHeight(n.left), TreeHeight(n.right)));
  }

7. Expression Tree

• An expression tree is a (binary) tree which represents a binary arithmetic expression (e.g. 3 * 5 - 2). All internal nodes in the expression tree are operators, and leaf nodes are the operands.

  

  Notice the tree respects operator precedence between * and -.

  NOTE: If the expression was 3 * (5 - 2), the tree above is not correct -- The correct tree is different.

• Postorder/inorder/preorder traversals over an expression tree will yield postfix/infix/prefix expressions.

Preorder:  - * 3 5 2
Inorder:   3 * 5 - 2
Postorder: 3 5 * 2 -