Use a quantum computer.
Quantum computers explore literally all possibilities
simultaneously.
They are theoretically possible,
but are at the cutting edge of physics.
It may (or may not) be feasible to build such a device.
Recursive Implementation of NFAs
An nfa can be implemented by means of a recursive
search from the start state for a path
(directed by the symbols of the input string)
to a final state.
Here is a rough outline of such an implementation:
function nfa (state A) returns Boolean:
local state B, symbol x;
for each l transition from state A to some state B do
if nfa (B) then return True;
if there is a next symbol then
{ read next symbol (x);
for each x transition from state A to
some state B do
if nfa (B) then
return True;
return False;
}
else
{ if A is a final state then return True;
else return False;
}
One problem with this implementation is that it could get into
an infinite loop if there is a cycle of l transitions.
This could be prevented by maintaining a simple counter (How?).
State-Set Implementation of NFAs
Another way to implement an NFA is to keep either a state set
or a bit vector of all the states that the NFA could be in at any
given time.
Implementation is easier if you use a bit-vector approach
(v[i] is True iff state i is a possible state), since most languages
provide vectors, but not sets, as a built-in datatype.
However, it's a bit easier to describe the algorithm if you use
a state-set approach, so that's what we will do.
The logic is the same in either case.
function nfa (state set A) returns Boolean:
local state set B, state a, state b, state c, symbol x;
for each a in A do
for each l transition from a
to some state b do
add b to B;
while there is a next symbol do
{ read next symbol (x);
B := f;
for each a in A do
{ for each l transition from a to some state b do
add b to B;
for each x transition from a to some state b do
add b to B;
}
for each l transition from
some state b in B to some state c not in B do
add c to B;
A := B;
}
if any element of A is a final state then
return True;
else
return False;
Formal Definition of NFAs
The extension of our notation to NFAs is somewhat strained.
A nondeterministic finite acceptor or nfa is defined by the
quintuple
M = (Q, S, d, q0, F)
where
- Q is a finite set of states,
- S is a finite set of symbols, the input alphabet,
- d: Q
´
( S
È
{ l } )
®
2Q
is a
transition function,
- q0 Î Q is the
initial state,
- F Í Q is a set of
final states.
These are all the same as for a dfa except for the definition
of d:
- Transitions on l
are allowed in addition to transitions on elements of S, and
- The range of d is
2Q rather than Q.
This means that the values of d
are not elements of Q, but rather are sets of elements of Q.
The language defined by nfa M is defined as
L(M) = {w Î
S*:
d*(q0,
w) Ç F
¹ f}
DFA = NFA
Two acceptors are equivalent if the accept the same language.
A DFA is just a special case of an NFA that happens not to have any
null transitions or multiple transitions on the same symbol.
So DFAs are not more powerful than NFAs.
For any NFA, we can construct an equivalent DFA (see below).
So NFAs are not more powerful than DFAs.
DFAs and NFAs define the same class of languages -- the
regular languages.
To translate an NFA into a DFA, the trick is to label each state in the
DFA with a set of states from the NFA.
Each state in the DFA summarizes all the states that the NFA might be in.
If the NFA contains |Q| states, the resultant DFA could contain
as many as |2Q| states.
(Usually far fewer states will be needed.)
From NFA to DFA
Consider the following NFA:

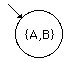 What states can we be in (in the NFA) before reading any input?
Obviously, the start state, A.
But there is a l
transition from A to B, so we could also be in state B.
For the DFA, we construct the composite state {A, B}.
What states can we be in (in the NFA) before reading any input?
Obviously, the start state, A.
But there is a l
transition from A to B, so we could also be in state B.
For the DFA, we construct the composite state {A, B}.
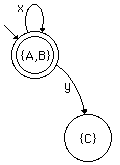 State {A,B} lacks a transition for x.
From A, x takes us to A (in the NFA), and the null transition
might take us to B; from B, x takes us to B.
So in the DFA, x takes us from {A,B} to {A,B}.
State {A,B} lacks a transition for x.
From A, x takes us to A (in the NFA), and the null transition
might take us to B; from B, x takes us to B.
So in the DFA, x takes us from {A,B} to {A,B}.
State {A,B} also needs a transition for y.
In the NFA, d(A,y)=C and
d(B,y)=C, so we need
to add a state {C} and an arc y from {A,B} to {C}.
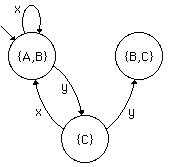 In the NFA, d(C,x)=A,
but then a null transition might or might not take us to B,
so we need to add an arc x from {C} to {A,B}.
In the NFA, d(C,x)=A,
but then a null transition might or might not take us to B,
so we need to add an arc x from {C} to {A,B}.
Also, there are two arcs from C labeled y, going to states
B and C.
So in the DFA we need to add the state {B,C} and the arc y
from {C} to this new state.
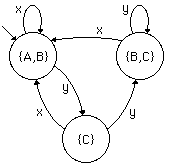 In the NFA, d(B,x)=B and
d(C,x)=A
(and by a l
transition we might get back to B), so we need an x arc
from {B,C} to {A,B}.
In the NFA, d(B,x)=B and
d(C,x)=A
(and by a l
transition we might get back to B), so we need an x arc
from {B,C} to {A,B}.
d(B,y)=C,
while d(C,y) is either B or C,
so we have an arc labeled y from {B,C} to {B,C}.
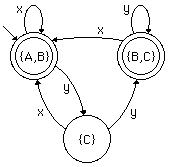 We now have a transition from every state for every symbol in
S.
The only remaining chore is to mark all the final states.
In the original NFA, B was a final state,
so in the DFA, every state containing B is a final state.
We now have a transition from every state for every symbol in
S.
The only remaining chore is to mark all the final states.
In the original NFA, B was a final state,
so in the DFA, every state containing B is a final state.
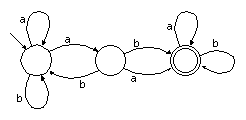 A state may have two or more arcs emanating from it
labeled with the same symbol.
When the symbol occurs in the input, either arc may be followed.
A state may have two or more arcs emanating from it
labeled with the same symbol.
When the symbol occurs in the input, either arc may be followed.
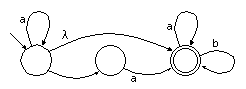 A state may have one or more arcs emanating from it
labeled with l
(the empty string) .
These arcs may optionally be followed without looking at the
input or consuming an input symbol.
A state may have one or more arcs emanating from it
labeled with l
(the empty string) .
These arcs may optionally be followed without looking at the
input or consuming an input symbol.
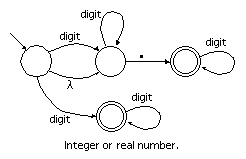

 What states can we be in (in the NFA) before reading any input?
Obviously, the start state, A.
But there is a l
transition from A to B, so we could also be in state B.
For the DFA, we construct the composite state {A, B}.
What states can we be in (in the NFA) before reading any input?
Obviously, the start state, A.
But there is a l
transition from A to B, so we could also be in state B.
For the DFA, we construct the composite state {A, B}.
 State {A,B} lacks a transition for x.
From A, x takes us to A (in the NFA), and the null transition
might take us to B; from B, x takes us to B.
So in the DFA, x takes us from {A,B} to {A,B}.
State {A,B} lacks a transition for x.
From A, x takes us to A (in the NFA), and the null transition
might take us to B; from B, x takes us to B.
So in the DFA, x takes us from {A,B} to {A,B}.
 In the NFA, d(C,x)=A,
but then a null transition might or might not take us to B,
so we need to add an arc x from {C} to {A,B}.
In the NFA, d(C,x)=A,
but then a null transition might or might not take us to B,
so we need to add an arc x from {C} to {A,B}.
 In the NFA, d(B,x)=B and
d(C,x)=A
(and by a l
transition we might get back to B), so we need an x arc
from {B,C} to {A,B}.
In the NFA, d(B,x)=B and
d(C,x)=A
(and by a l
transition we might get back to B), so we need an x arc
from {B,C} to {A,B}.
 We now have a transition from every state for every symbol in
S.
The only remaining chore is to mark all the final states.
In the original NFA, B was a final state,
so in the DFA, every state containing B is a final state.
We now have a transition from every state for every symbol in
S.
The only remaining chore is to mark all the final states.
In the original NFA, B was a final state,
so in the DFA, every state containing B is a final state.