CSC444 Homework #2 Answers

1. A man, a wolf, a goat, and a cabbage are all on one bank of a wide river. The man wishes to take himself and the three others across to the opposite side.

   The constraint is that there is only room in the boat for the man and at most one of the three others.

   The wolf and goat can't be left alone.

   The goat and the cabbage can't be left alone.

   The problem is to devise a plan to get all 4 to the other side.

   This problem can be solved using a finite state automaton:

     Notation:
     M : man
     W : wolf
     G : goat
     C : cabbage
   
   States: Pairs of subsets of {M,W,G,C} where the first subset of the
   pair represents which entities are on the initial side of the river and
   the second subset, the entities on the opposite side. For example, 
   
     MGC-W   means the man, goat and cabbage are on the initial side
             and the wolf is on the opposite side
   
   Input alphabet:
     ∑ = {m,w,g,c} where each input corresponds to an action:
   
               m: the man crosses the river by himself
               w: the man crosses with the wolf
               g: the man crosses with the goat
               c: the man crosses with the cabbage
    
   

   1. There are 16 possible "states", but some violate the constraints. How many possible states violate the constraints?

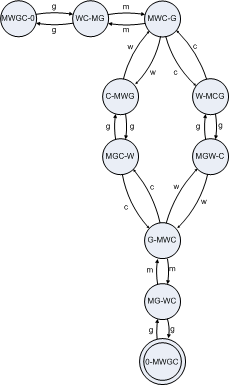
      Ans: 6. MC-WG, WG-MC, M-WGC, WGC-M, CG-MW, and MW-CG

   2. What is the start state?

      Ans: MWGC-0

   3. There is only one final state. What is it?

      Ans: 0-MWCG

   4. Construct the state diagram.You may omit the states and transitions that would violate the constraints.

      Ans:

      

   5. What is the minimum number of times the man must cross the river to get all 4 to the other side?

      Ans: 7

2. Exercises 1.3, 1.6b, 1.6c, 1.6e, 1.6f

1.3 The formal description of a DFA M is 
     ({q1, q2, q3, q4, q5}, {u,d}, δ, q3, {q3})
where the transition function δ is given by the following
     table. Give the state diagram of this machine.

         |   u    d
      ---|----------
      q1 |  q1   q2
      q2 |  q1   q3
      q3 |  q2   q4
      q4 |  q3   q5
      q5 |  q4   q5

Answer:

1.6 Give state diagrams of DFAs recognizing the following languages. 
    In all parts the alphabet is {0,1}


  b. { w | w contains at least three 1s }

Answer:

  c. { w | w contains the substring 0101, i.e., w = x0101y for some x and y }

Answer:

  e. { w | w starts with 0 and has odd length or 
           w starts with 1 and has even length }

Answer:

  f. { w | w does NOT contain the substring 110 }

Answer: