CSC444 Oct23

slide version

single file version

Contents

1. Exercises
2. Transitive Closure of a Relation
3. Product of Relations
4. Definition of R^k for a relation R.
5. Transitive Closure
6. R^* and R⁺ Relations on a Finite Set
7. Proof of Lemma
8. R^* and R⁺ for Finite Sets
9. R^* and R⁺ are transitive
10. Example 1
11. Example 2
12. Notation for relation R
13. Transitive Closure
14. Reflexive Transitive Closure
15. Sentences and Sentential Forms
16. Examples
17. Left Sentential Forms
18. Greibach Normal Form
19. Examples
20. Use of Greibach Normal Form
21. Converting to Greibach Normal Form: Preliminaries, Substitution
22. Substitution (continued)
23. Converting to Greibach Normal Form: Preliminaries, Left-Recursion
24. Eliminating Left-Recursion: Proof
25. Sketch of Conversion from CNF to GNF
26. Example
27. Example continued
28. Substitue for A's to get Greibach
29. Example: Summary
30. Derivation Length with Greibach Normal Form
31. Left Sentential Forms for a Greibach Normal Form Grammar
32. PDA Configurations

Exercises[2] [top]

Transitive Closure of a Relation[3] [top]

If R is a relation on a set A, R is of course not necessarily transitive.

At the other extreme, R is contained in A x A, and A x A is a transitive relation on A.

But A x A as a relation on A that contains R is too big to be of much use since by definition, (x,y) is in this relation for every x and y in A.

Instead what is often useful is the smallest transitive relation that contains R.

Product of Relations[4] [top]

If R and S are relations on a set A, the product of R and S, denoted by RS is defined by

  RS = { (x,y) | there is some z in A such that (x,z) is in R and (z,y) is int S }

Definition of R^k for a relation R.[5] [top]

If R is a relation on a set A, and k is any integer >= 0, define, a relation R^k inductively by:

   R0 = {(x,x) | x is in A }
   R1 = R
   Rk = Rk-1R for k > 1

Note that

   R2 = R1R = RR
   R3 = R2R = (RR)R

But by the associativity lemma, (RR)R = R(RR).

The associativity lemma means it doesn't matter what order you compute the products when computing R^k. So, for instance, we can unambigously write

  R3 = RRR

since (RR)R = R(RR)

Transitive Closure[6] [top]

For any relation R on a set A with n elements, define relations R⁺ and R^* on A by

  R+ = R1 ∪ R2 ∪ ... ∪ Rn-1 ∪ ...
 
  R* = R0 ∪ R1 ∪ R2 ∪ ... ∪ Rn-1 ∪ ...
 

R⁺ is called the transitive closure of R

R^* is called the transitive, reflexive closure of R

R^* and R⁺ Relations on a Finite Set[7] [top]

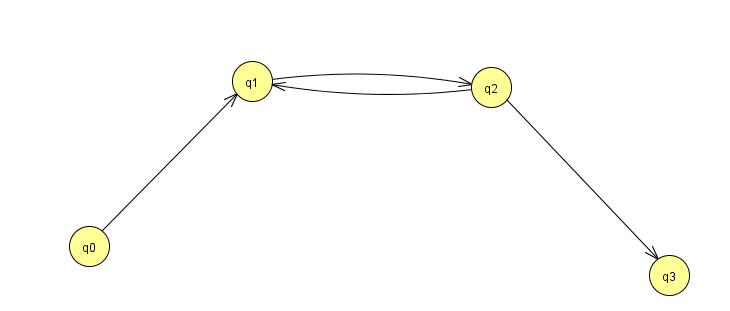
Example: R is the relation on the set A = {q₀,q₁,q₂,q₃} whose graph is shown below. That is, (q_i, q_j) is in R if there is a directed edge from q_i to q_j.

Note: In this example, 

1.  n = 4
2. (q0, q3) is in R5 (so m = 5):

   q0, q1, q2, q1, q2, q3 is a path of length 5 in the graph of R.

   (qi-1, qi) is in R for i = 1,2,3,4,5

   But q1 is the first element of A that is repeated later in this path
   so we can remove the elements between the first occurrence of q1 and
   the last occurrence:

3. q0, q1, q2, q1, q2, q3 is a path of length 3 in the graph
   of R.

   So (q0, q3) is also in R3 (So k = 3 < n = 4).

Proof of Lemma[8] [top]

R^* and R⁺ for Finite Sets[9] [top]

If R is a relation on a finite set A with n elements, then

  R+ = R1 ∪ R2 ∪ ... ∪ Rn
 
  R* = R0 ∪ R1 ∪ R2 ∪ ... ∪ Rn
 

R^* and R⁺ are transitive[10] [top]

Example 1[11] [top]

Example:
Let G be the following context-free grammar

 S -> E $
 E -> E '+' T | T
 T -> T '*' F | F
 F -> 'id' | '(' E ')'

Define a relation R on {S,E,T,F, '+', '*', 'id', '(', ')' }

By R = 
{
 (S,E)
 (E,E)
 (E,T)
 (T,T)
 (T,F)
 (F, 'id')
 (F, '(')
}

Is R transitive? No.
What is the transitive closure, R+

What is S R+ related to? That is, what are all the values
of w such that (S,w) is in R+

Answer: (S,E), (S,T), (S,F), (S, 'id'), (S, '(')

Example 2[12] [top]

Example:

Let G = (V, T, S, P) be a context-free grammar.

Define a relation R on (V ∪ T)* by

(α, β) is in  R if 

 1. α = uXv for some u, v in (V ∪ T)* and X in V, and
 2. β = uwv, and
 3. X -> w is a rule in P

Then, L(G), the language of G, is

  { w in T* | (S, w) is in R+ }

Note also that (S, w) is in R+ if and only if

  (S, w) is in Ri for some i >= 1.

Notation for relation R[13] [top]

The following notation will be also be used for the relation R of Example 2

 Notation: 
    For (x,y) in R, write x => y
    For (x,y) in Rk, write x =>k y
    For (x,y) in R*, write x =>* y
    For (x,y) in R+, write x =>+ y

Transitive Closure[14] [top]

Reflexive Transitive Closure[15] [top]

Sentences and Sentential Forms[16] [top]

Recall the relation R defined for a context-free grammar in Example 2:

Let G = (V, T, S, P) be a context-free grammar.

R is the relation on (V ∪ T)* defined by

  (α, β) is in  R, or equivalently, using the alternate notation,

  α => β

if 

 1. α = uXv for some u, v in (V ∪ T)* and X in V, and
 2. β = uwv, and
 3. X -> w is a rule in P

If S =>+ w and w is in T*, then w is a
sentence for the grammar G; w is in the language generated by G.

If S =>* w, where w is in (V ∪ T)*,
then w is called a sentential form for G.

Examples[17] [top]

Example
Let G be the following context-free grammar

 S -> E $
 E -> E '+' T | T
 T -> T '*' F | F
 F -> 'id' | '(' E ')'

then

(a) S =>3 T '+' T
(b) S =>+ T '+' T
(c) T '+' T is a sentential form

Left Sentential Forms[18] [top]

We can define a restricted version of relation => for context-free grammars for left-most derivatiosn.

Example 3

For a context-free gramar G=(V,T, S, P), 
define RL to be the relation on (V ∪ T)*
by

( α, β) is in RL if

 1. α = uXv for some u in T*, 
    v in (V ∪ T)* and X in V, and 
 2. β = uwv, and
 3. X -> w is a rule in P

Note: The only difference between relation R of Example 2 and
RL is in condition 1. For RL, u must consist of
only terminal symbols so that the X must be the left-most non-terminal
of α.

Greibach Normal Form[19] [top]

Examples[20] [top]

Use of Greibach Normal Form[21] [top]

Every context-free grammar can be converted to an equivalent grammar in Greibach normal form. The first step is to convert the grammar to Chomsky normal form!

If a sentence w for a grammar G has length n > 0 and G is in GNF, then any derivation of w must have length n.

Can you describe an algorithm that accepts any context-free grammar G and a string w of terminals and determines whether w is in the language of G? It doesn't have to be efficient, but ε grammar rules cause some problems.

Greibach normal form is useful in showing that any context-free language is the language accepted by some (nondeterinistic) push down automaton. (PDA).

Converting to Greibach Normal Form: Preliminaries, Substitution[22] [top]

Rules in context-free grammars are not required to meet in the Greibach normal from restrictions.

So to convert a given grammar G to Griebach normal form, we will need a way of replacing grammar rules, but the new grammar must be equivalent to G.

Substitution (continued)[23] [top]

Converting to Greibach Normal Form: Preliminaries, Left-Recursion[24] [top]

Eliminating Left Recursion

Eliminating Left-Recursion: Proof[25] [top]

Sketch of Conversion from CNF to GNF[26] [top]

Any grammar can be converted to Chomsky normal form. So G is assumed to already be in Chomsky normal form.

Rename the variables of the grammar if necessary as A₁, A₂, ...A_m

After the process below, only rules of this form will remain

• A_i -> A_ju with i < j
• A_i -> tu, with t i T and u in V^*
• B_i -> u, with u in (V ∪ {B1, B2, ..., B_i-1} )^* and u does not begin with any B_j

for k = 1 to m 
{
  for j = 1 to k - 1
  {
     for each Ak -> Aju
     {
       for all Aj -> v
       {
         add Ak -> vu
         remove Ak -> Aju
       }
       
     }
     for each Ak -> Aku
     {
       add rules Bk -> u and Bk -> uBk
       remove Ak -> Aku
     }
     if ( Bk was added ) {
       for each Ak -> v where v does not start with Ak
       {
         Add Ak -> vBk
       }
     }
  }
}

Example[27] [top]

A1 -> A2A3 | x
A2 -> A2A3 | x
A3 -> A4A5
A4 -> +
A5 -> x

Griebach: First Step

The rules for variables A₁, A₂, ... A₅ will be modified one at a time so that when A_k is modified

1. all rules of the form A_i -> A_ju with i less than k have i < j.
2. For a rule of the form A_k -> A_iu with i < k, substitute for A_i and repeat until the only rules for A_k of the form A_k -> A_iu have k <= i.
3. For a left recursive rule for A_k use the left-recursion elimination lemma, introducing new variable B_k

After the rules for each A_i will be in the correct form, beginning with a terminal followed by 0 or more variables.

The rules for the B_i's will either be in the correct form or be a string of variables beginning with some A_i. Substitute all the right side choices for A_i in this rule for B_i.

Example continued[28] [top]

A1 -> A2A3 | x
A2 -> A2A3 | x
A3 -> A4A5
A4 -> +
A5 -> x

The rule for A₁ is not recursive and no index is < 1. So nothing to do for A₁.

A₂ does not require substitution since there is no rule of the form A₂ -> A₁..., but A₂ does have a recursive rule. So use the left-recursion elimination to get:

A1 -> A2A3 | x
A2 -> xB2 | x     // Replaced A2 -> A2A3 | x
B2 -> A3B2 | A3   // 
A3 -> A4A5
A4 -> +
A5 -> x

Rules for A₃, A₄, and A₅ require no replacements.

Substitue for A's to get Greibach[29] [top]

A1 -> A2A3 | x
A2 -> xB2 | x     
B2 -> A3B2 | A3   
A3 -> A4A5
A4 -> +
A5 -> x

A₄ and A₅ rules are in Greibach normal form.

For A₃, replace leading A₄ on the right side.

A₃ -> +A₅.

Skip B₂.

A₂ rules are in Greibach normal form.

For A₁, replace leading A₂ on right side with all choices for A₂:

A₁ -> xB₂A₃ | xA₃ | x

Result:

A1 -> xB2A3 | xA3 | x
A2 -> xB2 | x     
B2 -> A3B2 | A3   
A3 -> +A5
A4 -> +
A5 -> x

Finally replace leading A₃ in rules for B₂

B₂ -> +A₅B₂ | +A₅

Example: Summary[30] [top]

A1 -> xB2A3 | xA3 | x
A2 -> xB2 | x     
B2 -> +A5B2 | +A5
A3 -> +A5
A4 -> +
A5 -> x

Derivation Length with Greibach Normal Form[31] [top]

The string x + x + x has length 5.

Give a derivation for x + x + x for the Greibach normal form grammar. How many derivation steps?

A1 -> xB2A3 | xA3 | x
A2 -> xB2 | x     
B2 -> +A5B2 | +A5
A3 -> +A5
A4 -> +
A5 -> x

Left Sentential Forms for a Greibach Normal Form Grammar[32] [top]

For a GNF grammar, every sentential form will be uv where u is a string of 0 or more terminals and v is a string of 0 or more variables!

PDA Configurations[33] [top]

For a PDA (Q, ∑, Γ, δ, q₀, F), we will consider triples (q, w, v) where q is in Q, w is in ∑^*, and v is in Γ^*. That is, we consider the set A = Q x ∑^* x Γ^*.

We define a relation R on A by:

Define

  (q,aw, Xv) is R-related to (p,w,uv)

if  δ(q,a,X) contains (p, u)

Note that a may be ε or an input symbol; that is a is in
∑ε 
  

The language recognized by the PDA can then be defined in terms of the transitive closure of R, R⁺.

  w is recognized by the PDA if

  (q0, w, ε) is R* related to (p, ε, u) 

  for some final state p.

Note that the stack doesn't have to be empty, although the PDA may
enforce this by not entering a final state unless the stack is empty.