Write a method isBST(Node t) that checks that the binary subtree at t is a binary search tree. The method should return true if t is the root of a binary search tree and false otherwise.

Assume Node has a field 'key' of Comparable class type Key.

You may use these private methods.
```
 private Node min(Node t)  // returns the  left-most Node in the subtree t
 private Node max(Node t)  // returns the right-most Node in the subtree t
	
```
(Each of these methods returns null if t is null.)

Note that an empty binary tree should be considered as a binary search tree.

Design a data structure that supports the following API for a generalized queue.

       public class GQ<Item item> 
---------------------------------------------------
       GQ()                // create an empty generalized queue
  Item get(int i)          // return the ith item from queue
  void add(Item item)      // append item to the end of the queue
  Item remove(int i)       // remove the ith item from the queue

Your data structure should implement all operations in logarithmic time (or better) as a function of the size of the queue.

Here is a sample client, showing the contents of the queue after each insertion / deletion.

  GQ<String> gq = new GQ<String>();
  gq.add("A");       // A
  gq.add("B");       // A B
  gq.add("C");       // A B C
  gq.add("D");       // A B C D

  String s1 = gq.get(2); // s1 = "C"
  gq.remove(2);          // A B D
  String s2 = gq.get(2); // s2 = "D"

Hint: GQ can store items in a private (ordered) symbol table with integer keys and values of type Item. When an item is added to GQ, put a (key, item) pair in the symbol table with key 0 if the symbol table is empty or with maximum key + 1, if not empty.

The GQ get(i) method cannot simply use the symbol table get.

Which of the following ordered symbol table implementations will you choose in order to met the performance requirement?

 private BinarySearchST<Integer, String> st;
 private BST<Integer, String> st;
 private RedBlackBST<Integer, String> st;

Give the implementation of add:
```
 public void add(Item item)
	    
```
Give the implementation of get.
```
 public Item get(int i)
	    
```
Give the implementation of remove.
```
 public Item remove(int i)
	    
```

Consider the 4-sum problem: Given N integers, do any 4 of them sum up to exactly 0?
- Consider the following brute-force solution (ignoring integer overflow).
```
   public static fourSum(int[] a) {
     int N = a.length;
     for (int i = 0; i < N; i++)
        for (int j = i+1; j < N; j++)
           for (int k = j+1; k < N; k++)
              for (int l = k+1; l < N; l++)
                 if (a[i] + a[j] + a[k] + a[l] == 0) return true;
     return false;
  }
```
  What is the order of growth of the worst-case running time?
```
 N, Nlog(N), N², N³, N⁴, 2^N
	    
```
- Describe an algorithm for 4-sum that runs in O(N²) time.
  
  Assume you have a hash-based symbol table and that put and get for integer keys are each O(1).
Below is the result of inserting a set of strings (and associated integer values) into search trie. The integer value is the order in which the string was inserted.
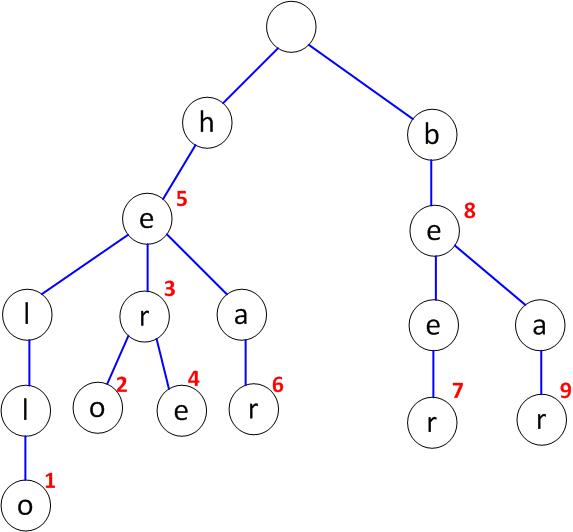
1. List (in alphabetical order) the set of strings that were inserted.
2. Add the string "hat" with value 10 and the string "happy" with value 11 to the trie and draw the new nodes required in the figure above.
Given the digraph below as an adjacency list and starting vertex 0, list the vertices in preorder and in postorder.
```
 0: 1, 2
 1: 2
 2: 3, 4
 3: 
 4: 3
	
```
Does this graph have a topological sort order? If so, give one such order. If not, give a directed cycle.

For the digraph in the previous problem, calculate the edgeTo array for the breadth first search method starting at 0; that is parameter s is 0.


private void bfs(Digraph G, int s) {
  Queue<Integer> q = new Queue<Integer>();
  marked[s] = true;
  q.enqueue(s);
  while (!q.isEmpty()) {
    int v = q.dequeue();
    for (int w : G.adj(v)) {
      if (!marked[w]) {
	edgeTo[w] = v;
	marked[w] = true;
	q.enqueue(w);
      }
    }
  }
}

 edgeTo[0] = --  (not assigned)
 edgeTo[1] = 
 edgeTo[2] = 
 edgeTo[3] = 
 edgeTo[4] =

Give the path from 0 to 3 determined by the edgeTo array.

Consider the following binary search tree method.


  public Key mystery(Key key) {
     Node best = mystery(root, key, null);
     if (best == null) return null;
     return best.key;
  }
  private Node mystery(Node x, Key key, Node best) {
     if (x == null) return best;
     int cmp = key.compareTo(x.key);
     if      (cmp < 0) return mystery(x.left, key, x);
     else if (cmp > 0) return mystery(x.right, key, best);
     else              return x;
  }

What does mystery(key) return?
1. predecessor of key
2. floor of key
3. ceiling of key
4. successor of key
5. the key in the symbol table that is equal to key if it is there or null otherwise.
What is the worst-case number of compares (the compareTo statement) for mystery? (Assume that the binary search tree is balanced.)
1. O(1)
2. O(log(N))
3. O(N)
4. O(N²)
5. O(2^N)

For each of the operations on the left, list which of the symbol table implementations on the right can be used to efficiently implement it. By efficient, we mean O(log(N)) or better on typical ASCII strings (in random order) where N is the number of keys in the data structure.

Assume that the data is ``random enough'' to avoid pathological cases. You may also assume uniform hashing.

For each question, you should write between one and five letters (A-E).

Choices
```
 A. Unordered array
 B. Ordered array
 C. RedBlackBST
 D. Separate-Chaining hashed symbol table
 E. Trie
	  
```
1. Get the value associated with a given key from the ST.
2. m Put a key (and associated value) into the ST; the key may already be in the ST, in which case the value is overwritten.
3. m Delete a key (and associated value) from the ST.
4. m Find the smallest key in the ST.
5. m Find the smallest key in the ST that is greater than or equal to a given string.
6. m Find the key in the ST that is the longest prefix of a given string.
7. m How many keys in the ST starts with a given prefix?