Definition: A binary search tree is a binary tree where each node has a Comparble key (and an associated value) and satisfies the restriction that the key in any node is larger than all the keys in nodes in its left subtree and smaller than all the keys in the nodes in its right subtree.

An ordered symbol table based on a binary search tree potentially has the advantages of both the ordered array implementation (BinarySearchST) and the linked list implementation (SequentialSearchST) without the disadvantages:

Advantages

• BinarySearchST: Fast searches: O(log(N))
• SequentialSearchST: Insertion doesn't require moving other key,value pairs.

Disadvantages

• BinarySearchST: Insertion can require O(N) moving of (key,value) pairs.
• SeqentialSerachST: Slow searches: O(log(N)) on average.

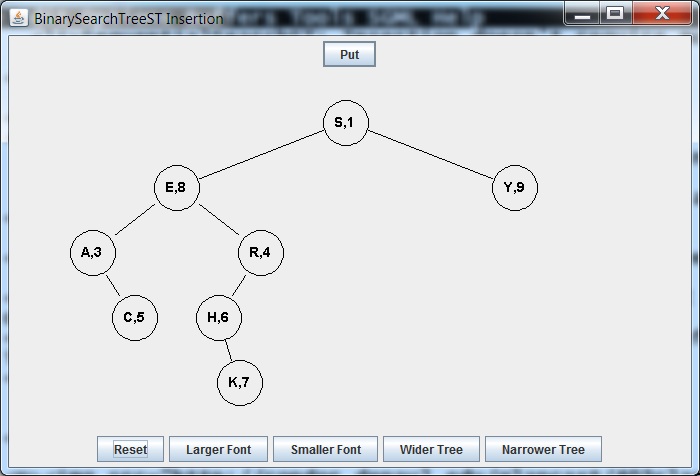
A binary search tree after inserting the keys: S E A R, in that order.

The value for a key is the number of insertions before and including the key.

      1  2  3  4
      S  E  A  R
    

What tree would you get if the insertion order was:

      1  2  3  4
      S  E  R  A
    

Same exact tree, but the values for R and A are swapped reflecting the order the keys were inserted.

But what happens if a key is inserted more than once? E.g., E is inserted twice for:

      1 2 3 4 5 6 7 8 9
      S E A R C H K E Y
    

The declaration of a generic binary search tree symbol table class should declare the generic parameters, Key and Value, so that elements of type Key are Comparable:

Non-static inner Node class

public class BST<Key extends Comparable<Key>, Value>
{

  private Node root;

  private class Node
  {
    private Key key;
    private Value val;
    private Node left;
    private Node right;
  
    public Node(Key k, Value v)
    {
      key = k;
      val = v;
      left = right = null;
    }

    public Node()
    {
      this(null);
    }	  
  }
}

A static inner class cannot access the (non-static) members of the containing class. But Node doesn't need to access these members - e.g. root. So Node could be static:

However, that means a static inner Node class has no access to the generic type parameters declared by the containing BST class.

So a static inner Node class must itself declare generic parameters:

public class BST<Key extends Comparable<Key>, Value>
{

  private Node<Key, Value> root;

  private static class Node<K, V>
  {
    private K key;
    private V val;
    private Node<K,> left;
    private Node<K,V> right;
  
    public Node(K k, V v)
    {
      key = k;
      val = v;
      left = right = null;
    }

    public Node()
    {
      this(null);
    }	  
  }
}

The get method returns the value associated with a key or null if the key is not in the BST.

To compute the value associated with a key in a BST:

• If the BST is empty, return null
• Else compare key with the root node
  • if key is smaller than root.key, the key has to be in the left subtree if it is present. So get the value from the left subtree.
  • else if the key is greater than root.key, the key has to be in the right subtree if it is present. So get the value from the right subtree.
  • else key is equal to root.key, so the value is root.val.

It is often convenient to write the operations on trees as recursive methods. This is because the tree is itself defined recursively.

Also the recursive code serves as an inductive proof of correctness.

• Base case: empty tree - just return null (obviously the code is correct for this case)
• The correctness of method get for a tree is reduced to the correctness for the smaller trees: the left subtree and the right subtree.

Inductively, the correctness of the subtrees can be reduced down to the base case, which is obviously correct.

These recursive methods generaly need to have a Node as a parameter!

Consequently, these methods can't be public.

So the pattern that arises is to have one public method that doesn't require a Node parameter and to have a private recursive method that is called to do all the work.

For example, here is a pair of get methods, one public and one private:

public Value get(Key k)
{
  // Call the private recursive find 
  // starting at the root of the tree.
  return get( k, root);
}

private Value get(Key k, Node t)
{
  if ( t == null ) {  // Base case
      return null;
  }
  if ( k.compareTo(t.key) < 0 ) { // reduce search to left subtree
      return get(k, t.left);
  }
  else if ( k.compareTo(t.key) > 0 ) { // or to the right subtree
      return get(k, t.right);
  }
  else  {
      return t.val;  // or Node with the key is found; return its value!
  }
}

Where is the maximum data element in a BST? the minimum data element?

These methods can easily be implemented either recursively or iteratively (using a loop) to move from the root to the largest (respectively, smallest) data element in the BST.

Using a binary search tree provides a nice improvement for the put method.

For the array implementation, we have to move all larger keys, but not for the binary search tree.

The put method again searches efficiently, but it doesn't have to move any other keys.

So the code is just a small variation on the recursive code for the get method:

• If the BST is empty, just create a new Node with this key,val pair and assign this Node to root.
• else if key is smaller than root.key, the key has to be in the left subtree if it is present. So put the key,val pair in the left subtree.
• else if key is greater than root.key, the key has to be in the right subtree if it is present. So put the key,val pair in the right subtree.
• else key is equal to root.key, so replace root.val with val.

Again, the recursive code serves as an inductive proof of correctness.

As for the get method, we write a public and a private version of get.

Execution of the public get and put begin at the top of the tree. The for the recursive private methods:

Code in the recursive method that comes before the recursive call corresponds to actions while going down the tree.

Code in the recursive method after the recursive call corresponds to actions while returning back up the tree

public void put(Key k, Value v)

That is, move through the tree as if you were searching for k. When a null reference is reached, attach a new node containing k and v.

A recursive version again uses a pair of methods. The public method return type is void, but the private method returns a reference to the root Node of the modified subtree into which the data was inserted:

  public void put(Key k, Value v)
  {
    root = put(k, v, root);
  }
  private Node put(Key k, Value v, Node t)
  {
    if ( t == null )
	t = new Node(k,v);
    else if ( k.compareTo(t.key) < 0 ) {
	t.left = put(k, t.left); // (***)
    }
    else if ( k.compareTo(t.key) > 0 ) {
	t.right = put(k, t.right);
    }
    else {
	// k is already in the tree;
        // update k's value
        t.val = v;
    }
    return t;
  }

(***) Before the recursive call we are going down the tree to insert (k,v) in the left subtree, then after the return from the recursive call, we are returning back up the tree and (re)attach the modified left subtree as t's left child.

Here is an iterative version of the public put method (no private method used):

The correctness is not quite as clear to demonstrate as for the recursive version.

  public void put(Key k, Value v)
  {
    if (root == null) {
       root = new Node(k,v);
       return;
    }
    Node p = root;
    while(true)
    {
      if (k.compareTo(p.key) < 0 ) {
	if ( p.left == null ) {
	  p.left = new Node(k,v);
	  return;
	}
	else
	  p = p.left;
      }
      else if ( k.compareTo(p.key) > 0 ) {
	if ( p.right == null ) {
	  p.right = new Node(k,v);
	  return;
	}
	else
	  p = p.right;
      }
      else { // k already in the tree, update its value
	p.val = v;
	return;
      }
    }
  }

As the code above reveals, insertion into a BST always occurs at a previously null link.

Deletion from a BST is more complicated. For example, what should happen if the data at the root is deleted?

Deletion is handled by considering three essential cases:

1. The BST is empty. 
	- Easy. Do nothing.

2. The data in Node t to be deleted has a null child (so 1 or 0 children)
	- Make the parent of t point to t's other child

3. The data in Node t to be deleted has two children. 
	- Find t's successor Node s (use private s min(t.right) )
	- Delete Node s from the subtree t.right (s has at most one child)
        - Replace t with s by setting s.right to the modified right
          subtree of t and setting s.left to t's left subtree.

Delete A

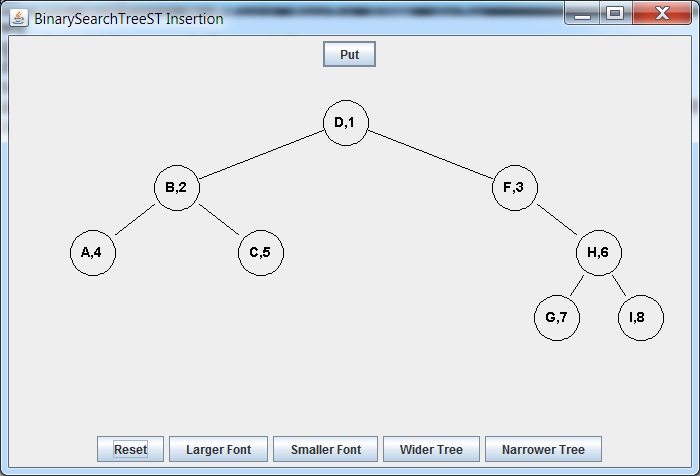
= delete A =>

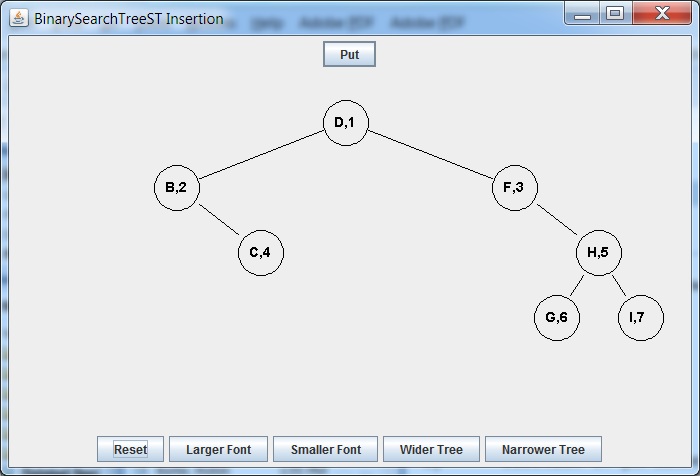
Delete F

= delete F =>

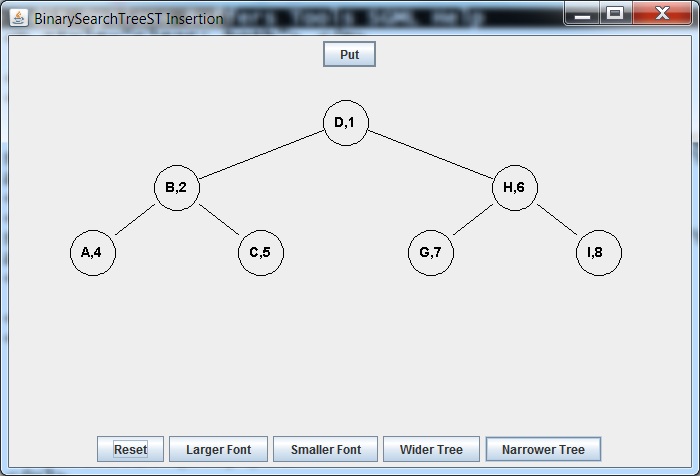
Delete D

Requires:

• Deleting successor F of D from the right subtree
• Replacing D Node with F Node

= delete D =>

• 3.1.8
• 3.2.1
• 3.2.2
• 3.2.3
• 3.2.6
• 3.2.14 (min)