Easy!

For a binary search tree with N keys and height, h, maximum height occurs if every node has a null link so that the tree is essentially a linked list:

 h = N - 1
    

The worst case number of comparisons for a search is height + 1.

So the worst case for an ordinary binary search tree is

      h + 1 = N
    

So the cost for the get method is O(N) in the worst case for a binary search tree.

A 2-3 tree is always perfectly balanced: For every Node, the height of its left subtree is the same as the height of the right subtree.

This guarantees that for a 2-3 tree with N nodes, and height h:

      N = 2(h + 1) - 1
    

So

 
      h = log2(N + 1) - 1 <= log2(N)
    

Note that N is the number of nodes, not necessarily the number of keys since each node can contain either 1 or 2 keys.

A 2-3 tree with no 3-nodes is a perfectly balanced binary search tree. So as just noted, for its height, h

      h <= log2(N)
    

where N is the number of Nodes. But if there are no 3-nodes, each node contains only 1 key.

So for such a perfectly balanced binary search tree

      h = O(log(N))
    

where h is the height and N is the number of keys

AVL trees are Binary Search Trees with the additional property that the methods maintain a "balanced" property:

      For every node in an AVL tree, the heights of its children differ by
      at most 1.
    

For the purpose of this definition (and also the implementation), an empty child will be considered to be at height -1.

The AVL tree below shows the height of each node.

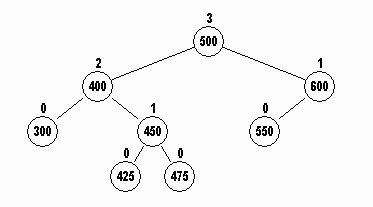
      The children of 600 have heights 

       0 (left child 550) and
      -1 (right child empty).

      and these differ by only 1.
    

For a perfectly balanced binary search tree with N keys we saw

 h = O(log(N))      
    

But what about the height of an AVL tree with N keys?

What is an upper bound for the height of an AVL tree with N keys?

This can be determined if we can answer the reverse question:

What is a lower bound for the number of keys in an AVL tree of height h?

Let N be the minimum number of keys that can be in an AVL tree of height h.

Fact

      2h / 2 < N
    

But this means

     h < 2log(N)  
    

Great! The height of an AVL tree is O(log(N)).

Since the height = O(log(N), this means the get method is guaranteed to be O(log(N)) for an AVL tree, even though it isn't perfectly balanced.

The put method first does a search and then either updates a value or else changes a few links to attach a new key value pair. Since the height is O(log(N)), this much would also cost only O(log(N)) for the put method.

However, the put method must also maintain the balance property. So we have make sure that doesn't add any more than O(log(N)) additional steps.

Maintaining the AVL Tree property, requires that the insert includes some code to rebalance portions of the tree if the property would otherwise be violated.

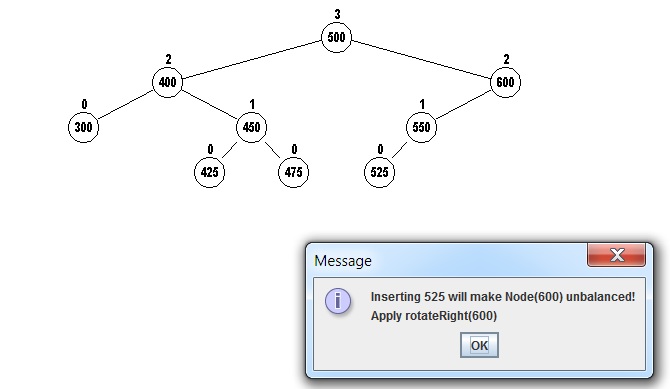
For example if we try to insert the value 525 into this tree in the usual way as a child of 550, the height of 550 would become 1, while the right child (empty) of 600 is still at height -1, a difference of 2.

So the node with 600 would become unbalanced!

This problem is solved by:

      1. First insert in the usual way for a binary search tree either in
      the left subtree or right subtree. (Duplicates are not allowed in
      this version.)
      2. Check if the heights of the two children subtrees differs by 2.
      If so, then rotate nodes to restore the AVL properties.
    

Two rotation methods are needed: rotateLeft or rotateRight.

To rebalance an unbalanced node requires we will need to either do one rotation or two rotations, depending on how the node became unbalanced.

The rotate methods are:

      1. private Node rotateLeft( Node p )

      2. private Node rotateRight( Node p )

    

Returning to the example AVL tree, we try to insert 525:

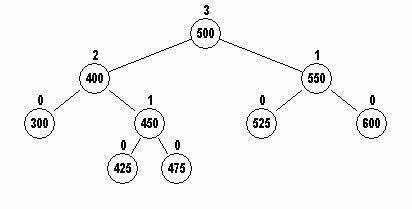
The rotateRight method below is called to rotate the node p to the right with its left child, 550 becoming the parent of 525 and 600:

If we try to insert 425 into this tree, node 500 would then violate the AVL condition. However, we can't use the rotateRight method:

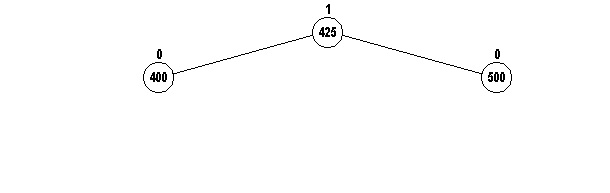
First rotate 400 to the left with its new right child (425), and then rotate 500 with its new left child (425 again in a new position) to the right to get:

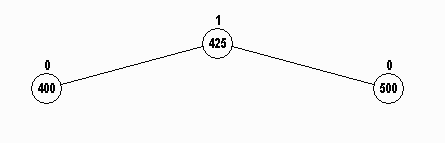
A slightly more typical example of two rotations is shown below. The value 450 is being inserted:

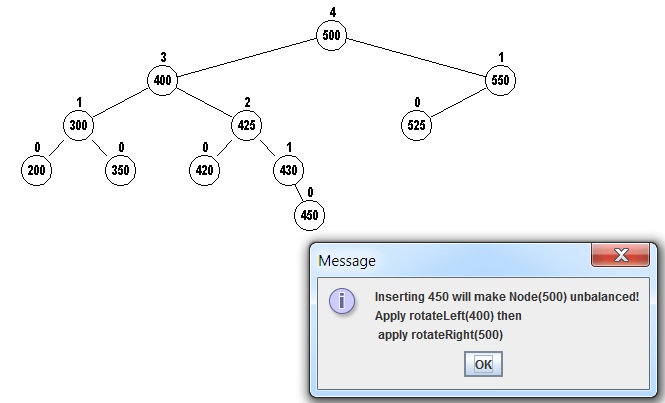
The rotateLeft will rotate 400 to the left, making 425 the new root of the subtree, then rotateRight will rotate 500 to the right making 425 the new root of the tree.

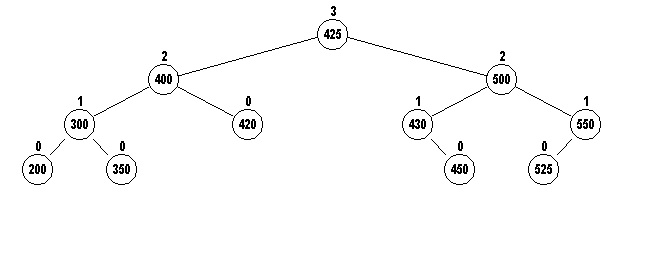
What happened to 425's previous left and right children?

Here is the method:

  private static Node rotateLeft( Node p )
  {
    // p's right child becomes the new subtree root
    Node r = ?;
    p.right = ?;
    r.left = ?;

    // Adjust the heights if 'height' is stored in the nodes.


    return r;
  }

Note: The height method is a static method that just returns the height of
the node passed to it, but also handles the case if null is
passed. In the later case, height returns -1.
    

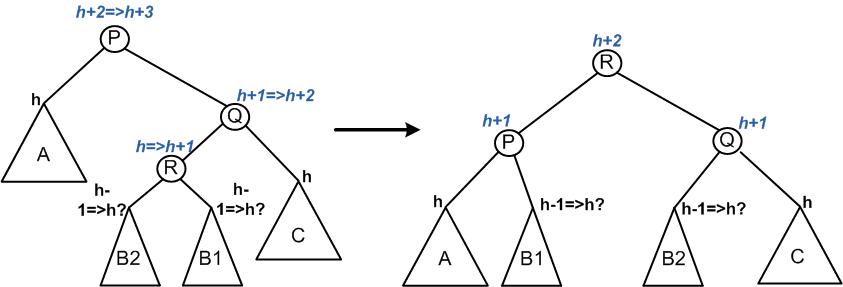
Two rotations are required:

 rotateRight Q
 rotateLeft P
    

 /*
      * item inserted to right of t and left of t.right.
      * node t is unbalanced and requires two rotations
      *
      * 1. rotate t.right to the right and attach the new subtree root to t.right
      * 2. rotate t to the left and return the new subtree root
      */

 


    

Assume a private Node class is used for an AVL tree class:

public class AVL<E extends Comparable<E>>
{
  // AVL members and methods
  ...

     // inner class
     private static Node 
     {
       public E data;
       public Node left;
       public Node right;
       public int height; // optional

       public  Node() {}
       public Node(E x) {
	 data = x;
	 height = 0; // optional
       }
     }
}
    

Recall insertion (without rebalancing) into a Binary Search Tree. We assume the BST has a private member root whose value is null if the BST is empty:

      private Node root;
    

public void put(Key k, Value v)
{
   root = put(k, root);
}

private Node insert(Key k, Value v, Node t)
{
  if ( t == null ) {
     t = new Node(k,v);
  } else if ( k.compareTo(t.key) < 0 ) {
     t.left = put(k, v, t.left);
  } else if ( k.compareTo(t.key) > 0 ) {
     t.right = put(k, v, t.right);
  }
  return t;
}
    

An AVL tree is a binary search tree with a balance condtition

The insertion for an AVL tree uses the same code as for any biinary search tree (above), but must add code to keep the AVL tree balanced and to compute changes in heights of nodes:

public void insert(E x)
{
   root = insert(x, root);
}

private Node insert(E x, Node t)
{
  if ( t == null ) {
     t = new Node(x);
  } else if ( x.compareTo(t.data) < 0 ) {
     t.left = insert(x, t.left);
     // If t is unbalanced call rotate method(s) to restore the balance
  } else if ( x.compareTo(t.data) > 0 ) {
     t.right = insert(x, t.right);
     // If t is unbalanced call rotate method(s) to restore the balance
  }
  // Recompute the height of t if height is member of Node
  return t;
}
    

Which rotation should be used when a node bcomes unbalanced depends on which child subtree (left or right) the offending value was inserted and which subtree (left or right) of that child.

Single rotation: rotateLeft(p) (changes 2 links)

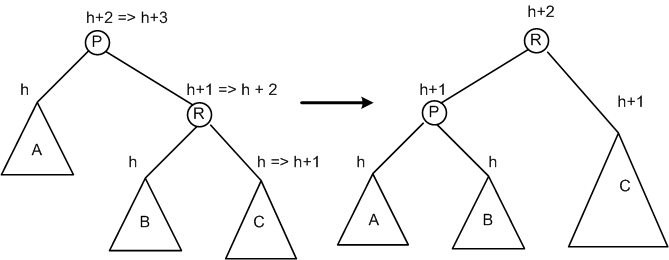
Double rotation: rotateRight(p.right), then rotateLeft(p) (changes 4 total links)

Here is a sketch of the proof that an AVL tree with N keys has height h = O(log(N)).

Let f(h) be the minimum number of keys in an AVL tree of height h.

(For example, try to draw AVL trees of heights 1, 2, and 3 with the smallest number of keys.)

      f(-1) = 0
      f(0) = 1
      f(1) = 2
    

For h >= 1,

      f(h) = 1 + f(h-1) + f(h-2)
    

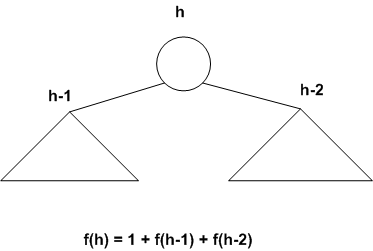
Since f(h-1) >= f(h-2), we get

      f(h) > 2f(h-2)   (for all h >= 1)
    

f(7) > 2f(5)	f(8) > 2f(6)
f(7) > 22f(3)	f(8) > 22f(4)
f(7) > 23f(1)	f(8) > 23f(2)
f(7) > 232	f(8) > 24f(0)
f(7) > 24	f(8) > 24

In general,

      f(h) > 2ceiling(h/2) > 2h/2
    

where ceiling(x) means the smallest integer that is >= x.

To print all the keys in a binary search tree in order, we should visit the nodes:

• left subtree, then
• the root, then
• right subtree

This is called inorder traversal.

For example, the keys() method of the binary search tree symbol table uses a private recursive method that visits the Nodes in preorder, adding them to a Queue or LinkedList.

Question: If the keys of a binary tree are output in inorder: 1 2 3 4 5 6 7, is the tree balanced (i.e., an avl tree)?

Uh, oh. The inorder output tells us nothing about the shape of the tree.

Preorder

Preorder just visits the root first:

• the root, then
• left subtree, then
• right subtree

Postorder

Postorder just visits the root last:

• left subtree, then
• right subtree, then
• the root

(Draw some examples)

If the preorder listing is given, can you determine the original tree?

Example

Preorder: 40 50 80 60 90

Draw the tree?

The level number (or depth) of a node in a binary search tree is the distance from the root.

Level order means to list the keys in order by their level and for keys on the same level, list them from left to right (that is, in increasing order).

Listing ALL the keys in a binary search tree in their usual order doesn't give any information about the shape of the tree. Is it balanced, essentially a linked list, or what?

However, if the keys are listed in level order you can use this as the INPUT order to rebuild the original tree! So instead of drawing binary search trees they can be described by giving the level order list of keys.

Level order of a binary search tree: 80 30 90 10 85 5 20 89 12.

What is the level order after inserting 70?

Level order of a binary search tree: 80 30 90 10 85 5 20 89 12.

What is the level order after Hibbard deletion of 5, 10 and 80?

(Hibbard deletion of a Node with 2 children replaces that Node with its successor.

Level order of a binary search tree: 80 30 90 10 85 5 20 89 12.

If we search for key 15, what keys in the tree are compared for this search miss?

What about a search for key 100?

Level order of a binary search tree: 80 30 90 10 85 5 20 89 12.

What is the level of key 20?

What is the height of the subtree at 20?

Level order of a binary search tree: 80 50 100 30 70 90 105 20 40 60 85 10

Is this an AVL tree?

Level order of an AVL tree: 80 50 100 30 70 90 105 20 40 60 85 10

The key 65 is inserted into this tree. Is a rotation required?