Mar 14

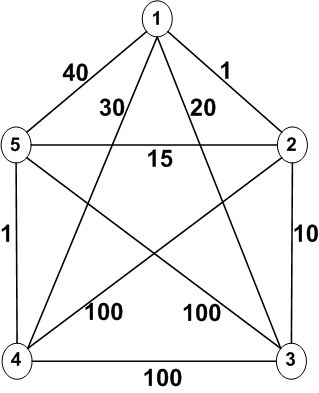
Starting at vertex 1, a greedy algorithm for the traveling salesman problem below would begin:

      1 => 2 => 3

Then the next vertex can't be 1. So the next vertex would have to be either 4 or 5.

       1 => 2 => 3 => 4 => 5 => 1
cost:      1   +  10   + 100  + 1 + 40 = 152

       1 => 2 => 3 =>  5 => 4 => 1
cost:    1  + 10 + 100 + 1 +  30 = 142

But a better path would be to start with the second smallest cost (20) from vertex 1:

       1 => 3 => 2 => 5 => 4 => 1
cost:    20 + 10 + 15 + 1  + 30 = 76

Example