Why should we study programming languages?
Office: CTI, Room 832
Office Hours: Monday, Wednesday 12:00pm - 2:00pm and by appointment
Email: lancaster@cti.depaul.edu
Phone: 312 362-8718
Fax: 312 362-6116
Imperative Paradigm: Perl (some C)
Functional: ML
Object-oriented: Java (some C++ and Perl)
There will be some programming assignments in Perl and in ML.
Sebesta, Concepts of Programming Languages, Addison-Wesley.
Randal L. Schwartz, Erik Olson and Tom Christiansen, Learing Perl on Win32 Systems, O'Reilly and Associates.
(Learning Perl instead of Learning Perl on Win32 Systems is satisfactory for our purposes.)
Ullman, Elements of ML Programmaing, Prentice-Hall.
Java or C++ through data structures.
That is, experience with an object oriented language - Java or C++ including standard abstract data structures: lists, stacks, queues, trees.
Homework: 40%
Midterm 30%
Final 30%
See
http://condor.depaul.edu/~glancast
Binary machine language: 01100001 01010001
Assembly language:
; code for A = A + B MOV A, r1 MOV B, r2 ADD r2,r1 MOV r1, A
Imperative programming: x = x + y;
Structured programming: while, for,
but goto considered harmful.
Functional programming: assignment considered harmful.
OO programming: encapsulate state and code together in objects.
Other paradigms...
Fortran I, Fortran II, Fortran IV, Fortran 77, Fortran 90
ALGOL 58, ALGOL 60, ALGOL W
Pascal, MODULA-2, MODULA-3, Oberon
CPL, BCPL, B, C, ANSI C
BASIC, Visual Basic
COBOL
ADA
Perl
Lisp, Scheme, Common Lisp
ML, Standard ML, CAML, ML97
Lazy ML
Miranda
Haskell, Gofer
Simula
Smalltalk
C++
Eiffel
Java
AspectJ
Perl
Objective Caml
Logic
Concurrent
Constraint
Visual
Syntax
Control Structures
Data types
Support for Abstraction
Expressiveness
Type System
Efficiency
Application Domain
Available Hardware
Programming Methodology
Implementation Methods
Programming Environments
Programming languages are much higher-level now than in the 1950s.
Machine architecture hasn't changed much (additions: virtual memory, caches, pipelines).
How do we get from high-level:
x := y + z;
to low-level:
MOV X R1 MOV Y R2 ADD MOV R3 Z
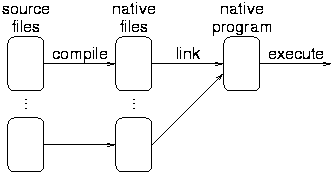
Compilers use the traditional compile/link/run strategy:

Examples: C, C++, ML.
Interpreters execute the source code directly:
This can be on the order of 100 times slower than machine compiled code execution.
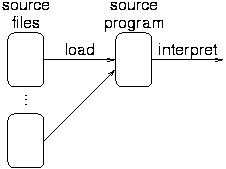
Examples: BASIC, Perl, TCL/Tk, ML.
Virtual machines (or interpretive compilers) use an intermediate byte code rather than native object code.
The source files are compiled (e.g. with javac) to the intermediate byte code. The byte code is then interpreted by the corresponding language specific interpreter program; e.g., java.
This is usually 'only' 10 times slower than target machine compiled code execution.
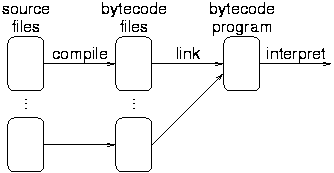
Examples: Pascal p-code, Java.
Just-in-time compilers are like VMs, but compile the byte code to native code:
This speeds up execution to about 5 times slower than machine compiled code execution.
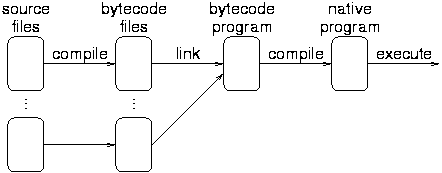
Examples: Java.
Syntax: does it `look like a program'?
tmp = x; // Looks like two assignments in Java x = y; but x = y // Doesn't look like an assignment; semicolon is missing y = tmp;
Static semantics: does it compile?
int[] x;
int y;
x = y; // Looks like an assignment, but doesn't compile because
// types of x and y are incompatible
Dynamic semantics: what does it do when it runs?
// syntax is ok and it compiles, but
Emp e;
Manager m;
e = new Emp("Bob");
m = new Manager("Ted");
e.display(); // What 'display' method should this use (Emp's or
// Manager's) at run time?
e = m;
e.display(); // Same expression at compile time; which 'display'
// should be used at run time.
Tutorials
Reference Manuals
Formal Definitions:
In this course, we shall concentrate on syntax, and `wave our hands' about the other two.
The lexical structure of a program defines the lexical tokens of the language including:
if or returnx or fish( or ;+ or /3.14 or "fish"For example:
return -x;
the tokens are:
return (keyword)- (operator)x (identifier); (punctuation)The lexical structure also says which characters should be ignored, such as white space or comments.
The lexical structure of a language can be specified in a number of ways. For example, the lexical structure of identifiers in a given language might be described in three different ways:
Informally: Identifiers must begin with an alphabetic character, followed by 0 or more alphabetic characters, digits, or the underscore character.
<identifier> -> alpha <more>
<more> -> alpha <more> |
digit <more> |
_ <more> | λ
where
alpha represents any character in the set
{a, b, ... , z , A , B , ... , Z},
digit represents any character in { 0, 1, ... , 9}, and
λ denotes the empty sequence of symbols.
Identifer = alpha ( alpha | digit | '_' )* alpha = a-z | A-Z digit = 0-9 The * means zero or more repetitions.
All three of these descriptions define a set of acceptable strings. The set of all these strings is called the associated formal language. For example, the following strings are acceptable:
a b1 euros HoBBit A__B
but not
@ 1b euro$ _HoBBit _A_B
The syntactic structure of a language specifies how and in what order the tokens or lexical elements may be combined into legal sentences of the language.
For program languages a formal sentence in this sense would be an entire program.
The syntactic structure, like the lexical structure can be described by a formal grammar, but in general not a regular grammar. Instead a second type of grammar is needed, a context-free grammar.
Once syntactic structure of an expression has been determined, the result is often represented as an abstract syntax tree.
For example, consider the expression:
( a + b ) * c
The lexical phase of a compiler identifies the tokens:
token type ( left parenthesis a identifier + operator PLUS b identifier ) right parenthesis * operator TIMES c identifier
The syntactic phase must determine that this sequence (in this order) is a valid expression and determine is syntactic structure (e.g., what are the operands of each operator). The result can be represented as an abstract syntax tree:
The abstract syntax tree can be used by the code generating phase of the compiler.
A postfix traversal of a binary tree will a) visit the left subtree, then b) visit the right subtree, and c) finally, visit the root of the tree.
A postfix traversal of the abstract syntax tree above for (a+b)*c can output code for a stack based interpreter like this:
Node Visited Output a Push a b Push b + Add c Push * Mult
A formal grammar is a 4-tuple (N, T, Start, P) where
A grammar rule or production is of the form:
a -> b
where, a and b are in (N union T)*
Note: The idea will be to use the rules on strings of symbols and this rule would say that the string a can be replaced by the string b.
This definition of formal grammars is too general for application to programming languages, which are more structured than natural languages.
Two special types of grammars are, however, useful. These are regular grammars and context-free grammars.
A context-free grammar is a grammar with the added restriction that the rules must all be of the form:
X -> b
where, X is in N, and b is still allowed to be in (N union T)*.
Example 1: A context-free grammar:
S ---> z A A ---> i A A ---> p
Example 1b: Essentially the same grammar as 1, but with BNF notation for the grammar:
<S> ---> z <A> <A> ---> i <A> <A> ---> p
Example 2: This grammar is also context-free.
S -> i S e S S -> i S S -> b
Example 3: This grammar is not context-free. Why?
S ---> aSBC | l CB ---> BC BB ---> b bB ---> bb bC ---> b
where l is the null string of symbols.
Consider expressions like
a + b * c ( a + b ) * c
Here are two possible grammars for such expressions. (Here 'id' represents any identifier, like 'a', 'b', etc.)
Grammar E1: E -> E + E | E * E | ( E ) | id
Grammar E2: E -> E + T | T (rules 1 and 2 for E) T -> T * F | F (rules 3 and 4 for T) F -> id | ( E ) (rules 5 and 6 for F)
The first would seem preferable, but it doesn't distinguish the precedence of * and +. It has another undesirable property as we will see. It is ambiguous about how to group the tokens of
ida + idb * idc
A regular grammar is a grammar where each rule must be of one of the following forms:
X -> t X -> t Y X -> λ
where X and Y are any elements of N and t is any element of T.
Note that X and Y are allowed to be the same non-terminal.
Example 1 (and 1b) above for context-free grammars are also regular.
Every regular grammar is also context-free.
Example 2 above is context-free, but not regular. Why?
See the sample programs: Lex.java and Parser.java.
The rules of a grammar provide a set of templates for forming grammatically correct sequences of terminals. Note that grammatically correct means with reference to this particular grammar.
Definition:
A sentence for a given grammar is a sequence of terminals which is grammatically correct for that grammar.
The language of a given grammar is the collection of all possible sentences for that grammar.
A derivation of a sentence is a sequence of steps that
Definition:
A sequence of terminal symbols is grammatically correct if and only if there is a derivation that produces the sequence as the result.
Notation
Each derivation step (replacement of a non-terminal symbol) is denoted by string-before-replacement => string-after-replacement
Example derivations for grammar of example E21 above:
Derivation 1:
Derivation of id + id:
Rule Used
E =>1 E + T 1: E -> E + T
=>2 T + T 2: E -> T
=>4 F + T 4: T -> F
=>5 id + T 5: F -> id
=>4 id + F 4: T -> F
=>5 id + id 5: F -> id
(The subscripts indicate the substitution rule that
was used at each derivation step.)
Derivation 2:
Derivation of (id):
Rule Used
E =>2 T 2: E -> T
=>4 F 4: T -> F
=>6 ( E ) 6: F -> ( E )
=>2 ( T ) 2: E -> T
=>4 ( F ) 4: T -> F
=>5 ( id ) 5: F -> id
Every derivation corresponds to a parse tree. The nodes of the parse trees are just the grammar symbols.
The root of the parse tree is the start symbol.
For each derivation step that expands a non-terminal, draw the non-terminal as a node with the expansion symbols its direct children.
The parse tree for "id + id":
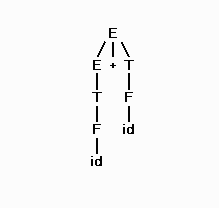
The parse tree for the derivation of "( id )" would be
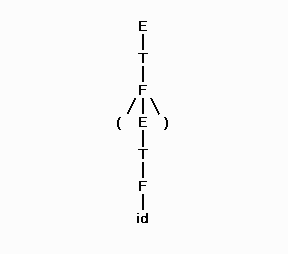
Here is the derivation of id + id given above:
Rule Used
E =>1 E + T 1: E -> E + T
=>2 T + T 2: E -> T
=>4 F + T 4: T -> F
=>5 id + T 5: F -> id
=>4 id + F 4: T -> F
=>5 id + id 5: F -> id
And here is another derviation of the same string,
E =>1 E + T 1: E -> E + T
=>4 E + F 4: T -> F
=>5 E + id 5: F -> id
=>2 T + id 2: E -> T
=>4 F + id 4: T -> F
=>5 id + id 5: F -> id
The first derivation is a left-most derivation and
the second is a right-most.
They differ only in the order that the nodes of the parse tree are expanded.
Derivations are perfectly suitable for defining sentences of a grammar.
However, derivations begin with the start-symbol and produce some sentence. This is backwards from what is required by a compiler or programmers.
Namely, the compiler is given a sequence of terminals (the source code of a program, partitioned into tokens).
It is not sufficient for the compiler to produce a derivation of some other valid program.
Instead of compiler error messages, would you be happy if the compiler reported, "I can't seem to comile your program, but here is a different program which I can compile. I hope you like it."
The parsing problem is to discover a derivation for a given input sequence.
Regular expressions represents sets of strings formed from some specified alphabet.
Sometimes the alphabet is just the set of all ASCII characters.
Three operations are defined on regular expressions to form new regular expressions:
Alphabet = Some set of symbols Operators: (1) concatenation, (2) alternation, (3) closure Operator Symbol -------- ------ concatenation (None, just write expressions next to each other) alternation | closure *
Here are some regular expressions defined over the alphabet { a,
b, c}
Set of Strings
Regular Expression Denoted by this Reg. Exp.
a { a }
b | c { b, c}
ab { ab }
a(b | c) { ab, ac }
(a | b)(c | d) { ac, ad, bc, bd }
a* { l, a, aa, aaa, aaaa, ... }
(a | b)* { l, a, b, aa, ab, ba, bb, aaa,
aab, aba, abb, baa, bab, bba,
bbb, aaaa, ... }
(ab | c)* { l, ab, c, abc, cab,
ababab, ababc, abcab, abcc,
cabab, cabc, ccab, ccc, ... }
It is not always easy to find a grammar even when you can describe the language informally.
However, if the language can be described by a Finite State Automaton, then it is easy to write the grammar.
Below is a simple FSA. I want to write a grammar that derives the same set of strings as are accepted by this FSA.
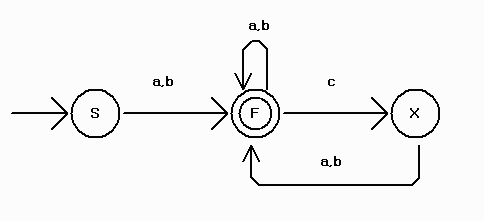
Grammar for this FSA is: S -> a F | b F F -> a F | b F | c X | l X -> a F | b F
What are the rules for convertin the FSA to a grammar?