
PointSet class
The PointSet class is a type that holds 2-dimensional points of type Point2D (NOT java.awt.geom.Point2D, but the Point2D in the algs4 project).
public class PointSet {
public PointSet() // construct an empty set of points
public boolean isEmpty() // is the set empty?
public int size() // number of points in the set
public void insert(Point2D p) // add the point p to the set (if it is not already in the set)
public boolean contains(Point2D p) // does the set contain the point p?
public void draw() // draw all of the points to standard draw
public Iterable<Point2D> range(RectHV rect) // all points in the set that are inside the rectangle
public Point2D nearest(Point2D p) // a nearest neighbor in the set to p; null if set is empty
public static void main(String[] args) // unit testing of the methods
}
In applications a set of "known" points is inserted into a PointSet instance, say ps. Then the PointSet methods support two main operations:
Given a Point2D q (usually not in the PointSet pset) find the point in pset that is "nearest" to q.
That is, find the point p contained in pset with the smallest value of p.distanceTo(q).
Given a rectangle find all the points in pset that are inside the rectangle.
The PointSet class method supports finding the nearest point with the method:
public Point2D nearest(Point2D p);
This method is implemented "brute force" in the PointSet class by simply evaluating the p.distanceTo(q) for ALL the Point2D points q in the PointSet and keeping track of the smallest distance.
The PointSet class uses a private ArrayList<Point2D> to store the points in the order they are inserted in the PointSet. So the "brute force" method just iterates through ALL the points in this ArrayList<Point2D> to find the nearest point.
The PointSet class method supports finding the points in a given rectangle with the method:
Iterable<Point2D> range(RectHV rect)
The return value of the range method is an object that has an iterator() method that iterates over all the Point2D points in the PointSet that are contained in the argument rectangle rect.
The implementation in PointSet just iterates through ALL the points in the ArrayList<Point2D> and checks if each Point2D p is contained in rect by using the RectHV method:
public boolean cointains(Point2D p)
If a point p is contained in rect, it is added to a LinkedList<Point2D> and this LinkedList<Point2D> is the actual Iterable<Point2D> object returned by the range method.
The PointSet and RectHV classes are provided.
KdTree Implementation
For this assignment you are to write a data type KdTree with the same public methods as PointSet to represent a set of points in the unit square. This class replaces the brute force approach of PointSet by implementing a binary tree (a 2d-tree) to hold the points instead of using an ArrayList.
A 2d-tree supports efficient nearest-neighbor and range searches that only have to examine a small subset of the points.
2d-trees have numerous applications, ranging from classifying astronomical objects to computer animation to speeding up neural networks to mining data to image retrieval.

Geometric primitives. Use the same classes for points and axis-aligned rectangles in the plane as in the PointSet brute force approach: Point2D and RectHV.

public class Point2D implements Comparable<Point2D> {
public Point2D(double x, double y) // construct the point (x, y)
public double x() // x-coordinate
public double y() // y-coordinate
public double distanceSquaredTo(Point2D that) // square of Euclidean distance between two points
public int compareTo(Point2D that) // for use in an ordered symbol table
public boolean equals(Object that) // does this point equal that?
public void draw() // draw to standard draw
public String toString() // string representation
}
public class RectHV {
public RectHV(double xmin, double ymin, // construct the rectangle [xmin, xmax] x [ymin, ymax]
double xmax, double ymax) // IllegalArgumentException if (xmin > xmax) or (ymin > ymax)
public double xmin() // minimum x-coordinate of rectangle
public double ymin() // minimum y-coordinate of rectangle
public double xmax() // maximum x-coordinate of rectangle
public double ymax() // maximum y-coordinate of rectangle
public boolean contains(Point2D p) // rect contains the point p (either inside or on boundary)?
public boolean intersects(RectHV that) // rect intersect that rectangle (at one or more points)?
public double distanceSquaredTo(Point2D p) // square of distance from point p to closest point in rectangle
public boolean equals(Object that) // does this rectangle equal that?
public void draw() // draw to standard draw
public String toString() // string representation
}
Do not modify Point2D or RectHV.
Replace the brute-force implementation. The KdTree class should have the same public methods as PointSet:
public class KdTree {
public KdTree() // construct an empty set of points
public boolean isEmpty() // is the set empty?
public int size() // number of points in the set
public void insert(Point2D p) // add the point p to the set (if it is not already in the set)
public boolean contains(Point2D p) // does the set contain the point p?
public void draw() // draw all of the points to standard draw
public Iterable<Point2D> range(RectHV rect) // all points in the set that are inside the rectangle
public Point2D nearest(Point2D p) // a nearest neighbor in the set to p; null if set is empty
public static void main(String[] args) // unit testing of the methods
}
Your KdTree implementation should substantially improve the execution time for the nearest(...) and range(...) methods. Using the 2d-tree will allow these methods to examine a small subset of the points instead of all the points.
2d-tree implementation.
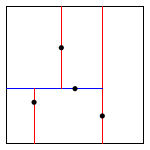
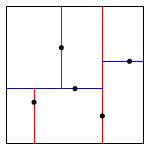
A 2d-tree is a generalization of a BST to two-dimensional keys. The idea is to build a BST with points in the nodes, using the x- and y-coordinates of the points as keys in strictly alternating sequence, starting with the x-coordinates.
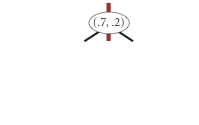
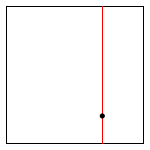
insert (0.7, 0.2) | 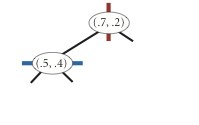
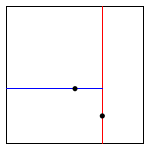
insert (0.5, 0.4) | 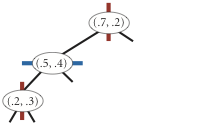
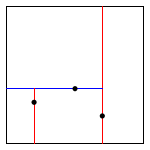
insert (0.2, 0.3) | 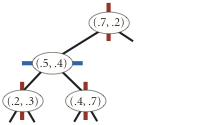
insert (0.4, 0.7) | 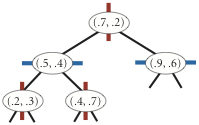
insert (0.9, 0.6) |
| 
| 
| 
| 
|
Draw. A 2d-tree divides the unit square in a simple way: all the points to the left of the root go in the left subtree; all those to the right go in the right subtree. At the next level of the tree, all points below go in the left subtree and all points above go in the right subtree and so forth, alternating depending on the depth. Your draw() method should draw all of the points to standard draw in black and the subdivisions in red (for vertical splits) and blue (for horizontal splits). This method need not be efficient—it is primarily for debugging.
The prime advantage of a 2d-tree over the PointSet's ArrayList is that it supports efficient implementation of range search and nearest neighbor search.
Important idea: Each node corresponds to an axis-aligned rectangle in the unit square, which encloses all of the points in its subtree.
The root corresponds to the unit square; the left and right children of the root corresponds to the two rectangles split by the x-coordinate of the point at the root; and so forth.
Each Node in the 2d-tree needs to hold a Point2D, left and right links. But the Node should also contain the depth in order to keep track of whether comparisons should be made on the x-coordinate or the y-coordinate of the Node point and the query point. If depth is even compare x-coordinates; otherwise, y-coordinates.
But you will also need to store the rectangle that corresponds to the Node point.
The root corresponds to the unit square.
The vertical line through the x-coordinate of the root's point divides the root's rectangle into two rectangles - one for the left child and one for the right child (if these are not null).

So here is a suggestion for the members of the Node class:
private class Node { private Point2D p; private Node left, right; private int depth; private RectHV r; private Node(double x, double y, int depth, RectHV r) { this.p = new Point2D(x,y); left = right = null; this.depth = depth; this.r = r; } }The Point2D class has 2 comparators:
Point2D.X_Order Point2D.Y_Order
For example to compare the x coordinates of two Pont2D points p and q:
if ( Point2D.X_Order.compare(p, q) < 0 ) {
// This means p.x is < q.x
}
You need to use Point2D.X_Order at Nodes with even depth and Point2D.Y_Order at Nodes of odd depth.
To simplify the coding, you can declare a static array, cmp, to hold these two comparators
private static Comparator<Point2D>[] cmp;
static {
cmp = new Comparator[2];
cmp[0] = Point2D.X_ORDER;
cmp[1] = Point2D.Y_ORDER;
}
The utility of this is illustrated by its use for the insert method:
public void insert(double x, double y)
{
RectHV r = new RectHV(0.0, 0.0, 1.0, 1.0);
root = insert(x, y, root, 0, r);
}
with private insert method that does all the work:
/** * * @param x the x coordinate of the point to insert in the subtree at t * @param y the y coordinate of the point to insert in the subtree at t * @param t the root node of the subtree * @param d the depth of t; * @param rect the rectangle for Node t * @return */ private Node insert(double x, double y, Node t, int d, RectHV prect)
The private insert can use the cmp array of comparators to write the same code to compare the query point x, y with the point in Node t by using the depth:
int axis = t.depth % 2;
Comparator<Point2D> cp = cmp[axis]; // cp is Point2D.X_Order if axis is even
// but Point2D.Y_Order, if odd
Point2D p = new Point2D(x,y);
Point2D tp = new Point2D(t.x, t.y);
int cmpval = cp.compare(p, tp); // Correct coordinate compare for depth of Node t
Range search.
To find all points contained in a given query rectangle, start at the root and recursively search for points in both subtrees using the following pruning rule: if the query rectangle does not intersect the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). A subtree is searched only if it might contain a point contained in the query rectangle.
The RectHV class supports checking intersections with the method:
public boolean intersects(RectHV otherRec)
Nearest neighbor search.
To find a closest point to a given query point, start at the root and recursively search in the subtree whose rectangle contains the query point; that is, at each node of the 2d-tree go left if the query point is less than the point in the node; otherwise go right.
Keep track of the minimum distance so far and the nearest point so far.
On the way back up the tree as the recursive method returns to a node from searching the selected subtree, you need to check whether you need to search in the other subtree. If the distance from the search point to the rectangle for the other subtree is is bigger than the minimum distance so far, you need not search the other subtree. Otherwise, you have to recursively search the other subtree as well.
To find the distance from a Point2D p to a RectHV rectangle r, use the RectHV method: r.distanceTo(p):
public double distanceTo(Point2D p)
The following files are included in hw5Files.zip. Point2D is in the algs4 project and is also in the zip file.
The JUnit test only checks that the methods have the correct result, not whether they are implemented using the 2d-tree. The NeighborTest and RectTest can be run with either your PointSet or KdTree. Both should be faster with KdTree.
The KdTreeApp1 and KdTreeApp2 applications may be somewhat useful for debugging as they draw points.
KdTreeApp1 displays the nearest neighbor for a randomly generated search point.
KdTreeApp2 displays a rectangle and redraws the points that are in the rectangle in RED.
This test inserts 1K, 10K, or 100K points into the data structure (PointSet or KdTree) depending on which input file is used (points1K.txt, points10K.txt, or points100K.txt). Then for each of 10000 query points, it computes the nearest neighbor among the points in the data structure.
The sample timings below were run in Eclipse with just-in-time compiling 'on' (the default).
With PointSet and points100K.txt
For 100000 points, nearest neighbor for 10000 query points: 7727msec
With KdTree
For 100000 points, nearest neighbor for 10000 query points: 71msec
Your times will depend on your machine, but KdTree should be faster.
This test inserts 1100000 points in the data structure. It draws the rectangle but only draws the points inside the rectangle.
With PointSet
For 1100000 points, computing 7836 points in rect(0.200, 0.200, 0.400, 0.600): 15msec
With KdTree
For 1100000 points, computing 7836 points in rect(0.200, 0.200, 0.400, 0.600): 6msec
Again your times will depend on your machine, but KdTree should be faster.
Submit KdTree.java file only to the dropbox for hw5.