CSC262 Assignment #2

Due Date: Friday, Jan 22

---

This assignment you will gain some practice creating and using dynamic arrays. There is only one program and it is partially written for you already to allow you to concentrate on the parts dealing with the dynamic array.

You will need to use the following features of C++

• new operator to create a two dimensional array during execution
• delete operator to release the memory created by new when it is no longer used.
• manipulating two dimensional (dynamic) arrays

Magic Square

You are to complete a program to create a magic square where the size of the square will be provided by the user during execution.

A magic square is a two dimensional integer array with n rows and n comums such that the sum of each row, each column, the main diagonal, and the opposite diagonal are all the same value.

For example, here is a 3 x 3 magic square. The sum of each row, each column, and each of the two main diagonals is 15.

   4   9   2
   3   5   7
   8   1   6
      

The provided file is magic.cpp. To complete the program, you need to provide effective implementations of these 3 functions:

     int **newSquare(int n);
     void makeMagic(int **m, int n);
     void deleteSquare(int **m, int n);
      

1. int **newSquare(int n);

This function should should use the new operator to create a two dimensional integer array with n rows and n columns and initialize each entry to be 0.

A "stub" definition of this function is provided in magic.cpp:

int **newSquare(int n)
{
  int** m;

  // Replace the next two lines
  cout << "newSquare not yet implemented" << endl;
  exit(0);

  return m;
}

This function will compile and the program will run as is. However, it will simply print a message and exit. You will need to replace the two lines indicated with code that actually creates the two dimensional dynamic integer array and initializes each element in this array to be 0.

A two dimensional dynamic array is created in two steps.

• First, create an array of int pointers. In the second step each of these will point to the first integer in an row.

   int **m;
   m = new int *[3];
  	  

  

• For each of these pointer variables, create an int array for the row and store its address in the pointer variable.

   for(int i = 0; i < 3; i++) {
      m[i] = ???  // Use the new operator again for the i-th row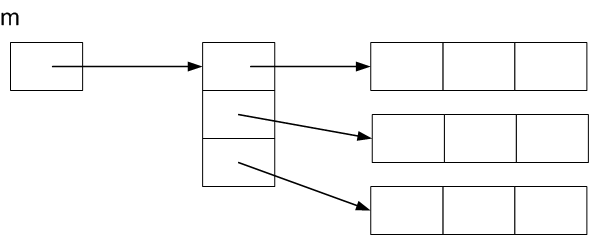
   }
  	  

  

  The variable m is declared to be a pointer to a pointer to int since its value points to a pointer!

• Finally, m can now be used as a two dimensonal array (with 2 subscripts).

  Write code to initialize each m[i][j] to be 0.

  

2. void deleteSquare(int **m, int n)

This function should release the two dimensional dynamic array created by newSquare after it is no longer needed.

The steps for deleting a two dimensional dynamic array are the reverse of the two steps for creating it:

• Delete each row array, then
• Delete the array of row pointers

Here is the "stub" provided in magic.cpp. You will need to replace the cout statement with the actual code to delete the dynamic array.

void deleteSquare(int **m, int n)
{
  cout << "deleteSquare not yet implemented" << endl;

}

3. void makeMagic(int **m, int n)

This is the function to fill in the n x n array m with the integers 1, 2, ... n*n so that the rows, columns, and two diagonals all add up to the same value.

Here is an algorithm that will allow you to do that in case n is odd. It is essentially the mirror image of the algorithm mentioned in the class notes, but it is a bit nicer to implement.

• Initially place 1 in the middle of the first row (row 0).
• After placing k at position m[i][j], place k+1 in the position that is 2 rows down and 1 column to the right, wrapping around if the row position or column position is off the array.

  If a value has already been placed at this position, then place k+1 at the position 1 row down (again wrapping around if necessary).

The row (and column) indices go from 0 to n-1. What is 1 position after n-1? Wrapping around means the next position is 0. The mod operator can easily handle this

For example if i is the current row and j is the current column, then the position one column to the right would have row ni and column nj given by:

	ni = i;             // Same row
        nj = (j + 1) % n;   // Next column, but wrap around if necessary
      

Sample Output 1

This program will create a magic square.
with n rows and columns for any odd integer n.


Enter number of rows desired: 3

   8   1   6
   3   5   7
   4   9   2

This a magic square!

Row Sums
sum of row  0: 15
sum of row  1: 15
sum of row  2: 15

Col Sums
sum of col  0: 15
sum of col  1: 15
sum of col  2: 15

Diagonal Sum: 15

Anti Diagonal Sum: 15
	
      

Sample Output 2

Enter number of rows desired: 5

  23  12   1  20   9
   4  18   7  21  15
  10  24  13   2  16
  11   5  19   8  22
  17   6  25  14   3

This a magic square!

Row Sums
sum of row  0: 65
sum of row  1: 65
sum of row  2: 65
sum of row  3: 65
sum of row  4: 65

Col Sums
sum of col  0: 65
sum of col  1: 65
sum of col  2: 65
sum of col  3: 65
sum of col  4: 65

Main Diagonal Sum: 65

Anti Diagonal Sum: 65

What to submit

Put your name in the space provided in the header comment and complete the code for the 3 functions in the file magic.cpp.

Be sure to test that your program works for n = 3, 5, and 7.

Submit your magic.cpp file to Course Online for Assignment #2.