Stacks and Queues
Linear Data Structure
A linear data structure is a collection of objects in which each object has a unique predecessor and successor. At most one object only has a predecessor without a successor (the last one) and there is at most one object can only have a successor and no predecessor (the first one).
One can implement it with either an array or a linked list. If one uses an array, then the predecessor of the ith object is the (i-1)st object, and its successor is the (i+1)st object. One thinks of it as
|
|
|
|
i-1 |
i |
i+1 |
|
|
|
|
If one thinks of it as a linked list, then one has
![]()
The arrow of each object points to its successor, and its predecessor is the object which point to it.
Linear data structures do not have to be finite. In fact, in theoretical computer science, an infinite linear data structure is used in the Turing Machine example. However, for our examples, we will assume that they are finite, so that there will be exactly one object with only a predecessor and no successor (the last one) and one object with exactly one successor and no predecessor (the first one). When one has a finite linear data structure, one can speak of the ends of it, corresponding to the first and last one.
When one has a first object and one uses arrays to implement it, there is a question of indexing the first one. The natural way is to indicate the first one by index one, but in implementations this depends on the computer language used. In Java, one tends to use 0 as the first index.
Stacks
A Stack is a linear data structure in which insertions and deletions are only done at one end. Typically, this is done at the last one. The end in which the insertions and deletions are done is called the top. This is because one thinks of a stack of dishes or trays as the model of a stack and one removes a disk from a stack of dishes only from the top. Insertions into the stack are traditionally called push, and deletions are traditionally called pop.
The picture one has in mind is:
Top
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The index 0 is at the bottom of the stack and the indices grow as one adds to the stack.
One can not see any of the values of the stack except by a pop operation, which removes the top element of the stack. Thus, we can not know what is the element just below the top of the stack except by removing the top two elements. Because one frequently wants to know what is at the top of the stack without having to remove it, one also has an operation of peek. Peek returns the value of what is stored at the top of the stack without removing it.
Finally, because we are implementing the stack inside a computer program, and everything has a finite limit, we have two operations to tell us about the state of the stack, namely stackFull and stackEmpty. StackFull returns true if the stack has no more room for expansion and returns false if it does have room. While stackEmpty returns true if the stack is empty and otherwise it returns false.
To see the UML of a stack (with the method search discussed below just before the section on Dequeues) click here, while to see the ADT of a stack, click here.
An example of an application using a stack is the infix to postfix conversion of arithmetic expressions.
Queues
A queue is a linear data structure where insertions are done at one end and deletions are done at the other end. The end in which the insertions are done is called the front, and the end where the removals are done is called the rear.
What should think of a queue as objects waiting in line, as for example, forming a line while waiting for a bus. The term queue comes from the English term which corresponds to a forming a line. Note that queue corresponds to an inventory system of first one in is the first one out (FIFO) and a stack corresponds to an inventory system of last one in is the first one out (LIFO).
Again, as with a stack, one can only know what is in a queue by removing an element from it. One has no access to the values of any element in the queue. As with a stack, one has a method of peek, which allows one to see the value of what is at the front of the queue without removing it. One also has the two methods of queueEmpty and queueFull, which return Boolean values of true or false depending if the query is satisfied or not.
The picture we have in mind for a queue is
front rear
![]()
![]()
|
|
|
V |
W |
X |
Y |
Z |
|
|
0 1 2 3 4 5 6 7 8
So V is at the front of the queue, followed by W, etc., and Z is at the rear of the queue. The peek method would return the value of V, and the remove or delete method would change the front to be W (by incrementing front by one) and return the value of V. Similarly, the insertion of a new element, say, AA would go into index 8 and rear would be incremented by one.
Notice that with our stack, as we add (push) or remove (pop) elements from the stack, the value of top increases or decreases. Hence, it will not be full until top has the value of the number of elements of the stack minus 1 (as we start the index at 0). I.e., we can have an arbitrary number of insertions and deletions to the stack as long as the number of elements in the stack does not exceed the allotted number of slots.
However, for our queue, this is not the case. For example, if we inserted AA and then BB to our queue above, they would go to positions 7 and 8 respectively:
![]() front rear
front rear
![]()
|
|
|
V |
W |
X |
Y |
Z |
AA |
BB |
0 1 2 3 4 5 6 7 8
However, if we now want to insert CC to our queue, we can increase the value of rear, as it is at the last element in our array. But there are two empty spaces at indices 0 and 1. So with this implementation we can insert at most 9 elements into the queue.
We get around this problem by having the queue wrap
around. 
Thus, an insertion of CC would go into position 0. I.e., we would add 1 to rear modulo 9, where 9 is the size of the array. We do the same for front. I.e., if we remove the element at index 8 (the last element in the array), we add 1 modulo 9 to front, so now it has value 0. With this implementation, the queue will only be full when it has 9 elements in it.
To see the UML of a queue, click here , while one can see its ADT by clicking here.
In practice, queues are usually implemented with linked lists. However, in this class, since we have not yet studied linked lists, we will implement them as arrays, which wrap around. So, for example, an implementation of insertion would look like (where front, rear, and size are class variables):
public boolean insertion(Object obj)
{
if (queueFull())
return false;
rear = (rear + 1) mod size;
queue[rear] = obj;
return true;
}
Note that for both stacks and queues, one wants to know if an element is in it. I.e., it belongs to the stack or queue. In theory, one can not know except by emptying it out. However, most implementations of stacks and queues allow the user to see if an element is there. I have done in the example via the method search. In Java, for the ArrayBlockingClass, the method is called contains. For the Stack class in Java, it is called search. However, the contains method only returns true or false depending whether it is in the queue or not, respectively. It does not give its position.
DeQueue
A dequeue is a linear data structure in which insertions and deletions can be done at both ends. (Some people pronounce it as “deck”.) The term dequeue comes from double ended queue. Thus, we no longer have a front and a rear, but many people still refer to the ends as front and rear, although leftmost and rightmost would probably be more apt.
An example of using a dequeue
is in the implementation of task scheduling for several processors. A separate dequeue with threads to be executed is maintained for each
processor. To execute the next thread, the processor gets the first element
from the deque (using the "remove first element"
dequeue operation). (In computing, when a process forks,
it creates a copy of itself.) If the current thread forks, it is put back to
the front of the dequeue("insert element at front") and the new thread is
executed. When one of the processors finishes execution of its own threads
(i.e. its dequeue is empty),
it can "steal" a thread from another processor: it gets the last
element from the dequeue of another processor
("remove last element") and executes it.
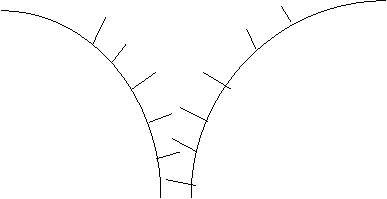
We can use railroad tracks to model the above 3 data structures:
Stack
Suppose A,B,C,D,E are the elements to be added and/or removed from the stack.
![]()
![]()
![]()

 ABCDE
ABCDE
![]()
If we do two pushes (push A and then B) we get the following picture:

 CDE
CDE

![]()
![]() B ß top
B ß top
A
Then if we do one pop and then another push, we have

 DE
DE
![]()

 A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() C ß top
C ß top
A
So the railroad siding plays the role of the stack.
Queue
For a queue, we just have a piece of the railroad tracks, where we suppose that A,B,C,D, and E are to inserted/removed from the queue.
![]()
ABCDE
![]()
Then if insert three elements (enqueue A, enqueue B, and enqueue C) we get:
F R

A B C DE
![]()
Then if we remove one element, we get:
F R

A B C DE
![]()
Finally, one adding another element we get:
F R

A B C D E
![]()
We can put the stack and queue together to yield:
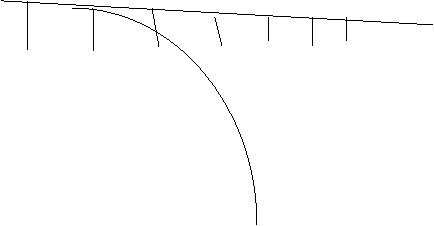
![]()
![]()
 ABCDE
ABCDE
![]()
Dequeue
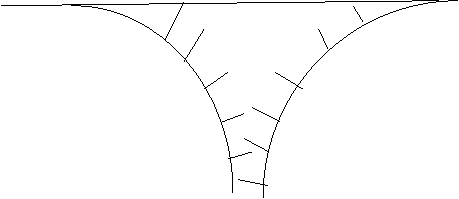
A dequeue is like a queue, except insertions and deletions can be done at both ends. So we draw it as a section of track with two other pieces for insertion at front and deletion at end.
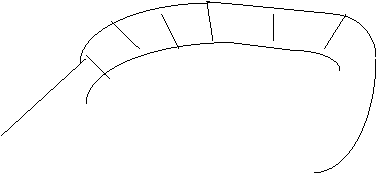
![]()
![]()
 delete from rear
delete from rear
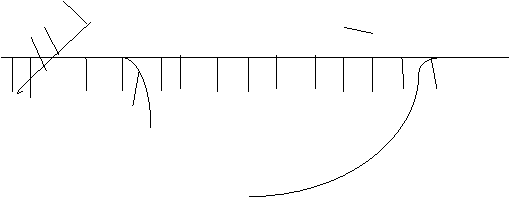
![]() ABCDE
ABCDE

![]()
![]()
![]()
![]()
![]() insert at front
insert at front
![]()
![]()
![]()
So if we first insert at rear, then insert at front we have:
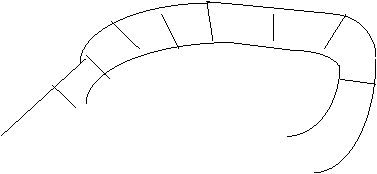
![]()
![]()
![]()
![]() F R
F R
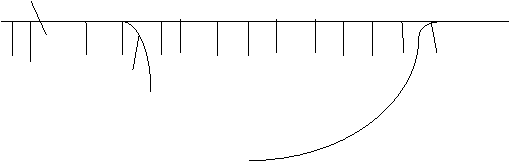
![]() B A CDE
B A CDE

Then a delete from the front and insert at the rear yields:

![]()
![]()
![]()

![]() F R
F R

![]() B A C DE
B A C DE

Finally, a delete from the rear followed by an insertion at the front and insertion at the rear gives:

![]()
![]()

![]() F
R
F
R
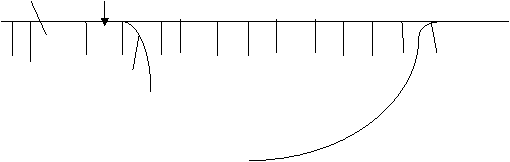
![]() BC D A
E
BC D A
E
