-
x = 70 inches
SDx = 3 inches
x = 162 pounds SDy = 30 inches
r = 0.5
- r = 0.0
- r = 1.0
- r = 0.5
-
y - y =
(r SDy / SDx)
(x - x)
-
76
67
70


x = 162 pounds SDy = 30 inches
r = 0.5


homoscedastic, which means "same stretch": the spread of the residuals should be the same in any thin vertical strip.
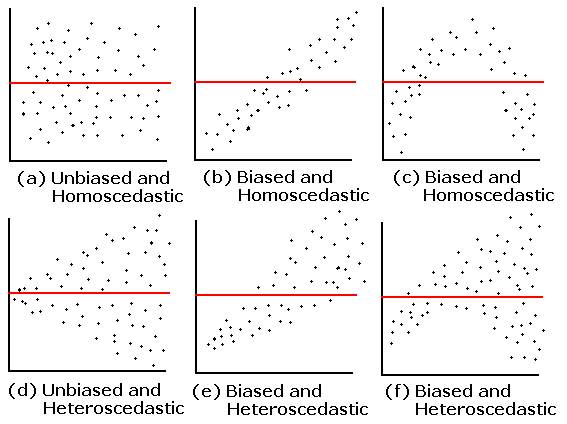
(b) Biased and homoscedastic. The residuals show a linear pattern, probably due to a lurking variable not included in the experiment.
(c) Biased and homoscedastic. The residuals show a quadratic pattern, possibly because of a nonlinear relationship. Sometimes a variable transform will eliminate the bias.
(d) Unbiased, but homoscedastic. The SD is small to the left of the plot and large to the right: the residuals are heteroscadastic.
(e) Biased and heteroscedastic. The pattern is linear.
(f) Biased and heteroscedastic. The pattern is quadratic.